フルリモートワークを利用して長野県を自転車で巡りながら仕事してみた

概要

自分が勤めている会社はフルリモートです。家以外に旅館、ネカフェ、コワーキングスペース等で働けます。

自転車旅が好きで有給を使い切ってしまったので仕事しながら自転車旅をしてみようと考え、本格的に寒くなる前に自転車を持って1週間ほど長野県に滞在してみることにしました。

準備

普段の自転車旅は旅にまつわる準備のみですが、今回は昼間に仕事するので仕事関連の準備も必要です。

  • 滞在する場所、仕事する場所の調査と決定
  • 上長へリモートワークする予定場所の共有
  • Macを破壊せずに運ぶ方法を考える
  • 仕事に必要な道具のリストアップ
  • その他考えること

滞在する場所、仕事する場所の調査と決定

自転車旅なのでいろいろな都市を転々としたいところですが、今回は初の試みなのでトラブル等で始業に間に合わないことを避けるために一つの都市を中心に留まりいろいろなところに行ってみることにしました。

以下の理由から長野県の塩尻、松本、安曇野辺りに滞在することにしました。

  • 今回の計画の前日まで長野県にいる
  • 自転車で諏訪以北に行ったことがない
  • ワインが好きで塩尻のワイナリーを巡りたい

仕事する場所については社内のルールと合わせて以下の条件で探しました。

  • ネットワーク環境がある
  • PCの充電ができる
  • 会議用の部屋もしくは他の人に会話を聞かれない環境がある
  • 始業時間から終業時間まで営業している
  • 1日の利用料が3000円以下

ネットワーク環境がある、PCの充電ができる

コワーキングスペースは場所によって値段もルールも設備も全然違うので一つ一つ調べる必要があります。ただし、コワーキングスペースなので電源やネット環境は共通して用意されていました。

会議用の部屋もしくは他の人に会話を聞かれない環境がある

会社のルールで他の人に会話を聞かれない環境で会議をする必要があるため、一人でも借りれる会議室があるかどうかも条件に入ります。会議室を有料にしているコワーキングスペースが結構あるのでその辺も気にしながら探しました。

始業時間から終業時間まで営業している

始業時間から終業時間まで営業していることですが、始業時間については10時半からで他の会社に比べると遅めだと思うのでこれは特に問題になりませんでした。

しかし、10時半始業の場合、終業時間は19時半なのでそれまでやっているコワーキングスペースは結構限られました。行政系のコワーキングスペースは17時までの場合が多くてコアタイムが16時半とはいえさすがに1日の就業時間が短すぎてしまうので候補からは外れました。

1日の利用料が3000円以下

1日あたりの値段が3000円以上の場所は考えていませんでした。快活クラブの鍵付き個室の9時間パックが2700円くらいなのでそれよりも安い場所じゃないと快活クラブに行けばいいだけの話になるのでそれ以下で考えていました。

今回利用したコワーキングスペース

以上の条件で探した結果、今回利用したコワーキングスペースは以下でした。 33gaku.jp

  • 1日1000円で利用できる
  • 会議室があって無料で利用できる
    • 前日から予約しておけるので、先客がいて使えないということがない
  • 19時まで営業(終業時間30分前だが、フレックスなので問題なし)

特によかったのが利用料金でした。会議室が無料なのも嬉しいです。 快活クラブは毎日利用するとなると4日で10000円を超えてしまうのでそう考えるとかなりお得です。

上長へリモートワークする予定場所の共有

会社のルールで上長に何日にどこでリモートワークするかを伝える必要があります。 早朝にどこ走るかを大体決めて、そのルートから快活クラブに行くか、コワーキングスペースに行くか決めました。

Macを破壊せずに運ぶ方法を考える

どうやって運ぶか

背中にリュックを背負って自転車を漕ぐと背中が蒸れてしまうので、自転車旅をするときは自転車に荷台を取り付けてその荷台にパニアバッグをつけて荷物を運びます。

しかし、今回持っていく仕事用のMacはパニアバッグに入れておくと自転車の振動で壊れたり、自転車から離れた際に盗難にあったりするリスクがあるため、リュックを背負ってその中にMacを入れて常に肌身離さないようにしました。

破壊対策

自転車旅はいろいろなものを持っていきますが今回初めて持っていくMacは様々な荷物の中で最も脆くて高価なので、破壊しないようにいろいろ用意しました。まずは本体を守るためにカバーを買いました。

www.amazon.co.jp

安くて軽いのでこれで完全に守れるとは思わないですが細かいキズがつくのを防げるくらいにはなると思います。 あとは内側がクッションになっているPC用のバッグです。

これも安物ですがないよりはマシなのとポケットがついているので周辺機器などを入れたりできるのが便利です。

あとは家にある100均座布団2つでMacを挟んでリュックに入れました。

自転車から落車して背中から落ちたらどんな対策をしていてもジ・エンドな気がしますがその場合は仕方ないです。

仕事に必要な道具のリストアップ

仕事関連のものは以下を持っていきました。

  • Mac
  • Macの充電器
  • PC用バッグ
  • 骨伝導イヤホン
  • 骨伝導イヤホン用充電器
  • スペア用イヤホン
  • 覗き見防止フィルター

特別なものは特にないですね。骨伝導イヤホンの充電がないなどの不測の事態に備えて予備イヤホンを一応持っていったくらい。 あとは会社のルール上、覗き見防止フィルターは必須なので持っていきました。

その他考えること

完全密室のネカフェではあまり考える必要ないかもしれないですが、

  • チャリ乗った後の汗の臭いや服装
  • 駐輪場の有無

などは考えました。チャリ乗った後の汗は予備の文明服を持っていく余裕はなかったので汗拭きシートや制汗スプレーを使う程度でそのままピチピチのサイクルジャージで仕事してました。気にする人は余裕を持って始業前に銭湯に行ったり、文明服を持って行ったほうがいいかもしれないです。

駐輪場があるかどうかはコワーキングスペースのサイトに書いていないことが多かったですが、事前に電話したら教えてくれました。今回行ったところは駐輪場がありました。

平日の1日の流れ

走る時間確保のために4時半か5時くらいに起きます。

テントを片付けて荷物を自転車に取り付けて出発します。

コンビニで朝ごはんを済ませて走り出します。サイクリングロードや景色のいい山を登ったりして大体40kmくらい走ります。

コンビニで第2の朝ごはんを済ませてから今日の仕事場であるネカフェかコワーキングスペースに行きます。

仕事します。昼休憩は事前にコンビニで買ったものを食べます。途中退室もできるので近所のラーメン屋に行ったりもしました。 ネカフェにはシャワーがついているのでこのタイミングで浴びたりします。

退勤します。ネカフェは9時間を超えると10分ごとに延長料金かかるので1分も残業は許されません。

夕食は外食します。

温泉に行きます。シャワーを浴びている場合は入らないこともあります。

泊まる公園を見つけてテントを張ります。

特にやることもないので大体21時か22時位には寝ます。

トラブル

初日からパンク

三連休明けの火曜日、雨上がりの濡れた国道を走っているときに突き刺しのパンクをしました。 15分程度足止めくらいましたが、その後は特に問題なく約40km走りました。

テントポールの盗難

高ボッチ高原を登ることを予定していました。行って同じ道を戻るだけだったので荷物を軽くするために登っている途中でテントや衣類、寝袋などを茂みに置いていきました。高ボッチ高原を登って下ってくると荷物が荒らされた形跡があって中のテントポールと工具類がなくなっていました。

被害届を出して後日長野に滞在している間に工具類は見つかったので警察署で回収できましたが、テントポールと犯人は現在も見つかっていません...

テントポールがないとテントが建てられないのでその後は直接地べたにマットを敷いて寝袋に包まって寝ました。

感想

少々トラブルはありましたが、業務に支障が出ることもなくかつ自分が行きたいと思っていたところには大体行けたので結果的には成功でした。

1日1000円のコワーキングスペースがあったのもよかったです。地理的に今回利用しなかったですが、条件に合致する安いコワーキングスペースは他にもあったので、次は1つの街に留まらず街を転々としながら長距離移動でやってみたいです。

まとめ

よかったところ

  • 体力的にきついかと思ったが毎日40km安定して走れた
  • 業務に支障がでなかった
  • 自転車+仕事でも毎日8〜9時間睡眠できた
  • 同じ街に留まったので地元のグルメもいろいろ味わえた
  • 1週間でも地理を結構覚えて走りやすいところがわかってきた

課題点

  • Mac背負って走るのはしんどい
  • 一人+仕事道具で荷物が多くてバッグに余裕がない
  • 毎日ネカフェだとお金がかかる

Mac背負って走るのはしんどい

リュックに背負うとどうしてもMacは重いです。 平地ならまだしも登りとかだと腰が破壊されます。

自転車に取り付けるにしても、自転車離れる際にMacをわざわざ持っていく必要があるのが大変ですね。 アイデアとしては自転車に取り付けられてリュック化できるようなバッグを使うとかですかね...

一人+仕事道具で荷物が多くてバッグに余裕がない

10月で長野県だと夜寝るとき寒いので寝袋も大きくて衣類も嵩みがちです。 一人だと荷物の分散もできなく、更に仕事道具もあったので余裕はありませんでした。 自炊もしたかったのですが、自炊道具を入れるだけの余裕はありませんでした。

現在は自転車の後ろだけ荷台があるので前にも荷台をつけるなどしたらもっと収納できるようになるのでそれも検討します。

毎日ネカフェだとお金がかかる

ネカフェだと安定して仕事できる環境があるので計画に組み込みやすいですが、やはり料金が高いです。 4日で1万超えなので今後1週間以上の行程だと予算をかなり圧迫してしまいます。

次行くときは極力ネットカフェより安いコワーキングスペースを利用するように計画したいですね。

TypeScript + Node.js + D3.js を使って白地図に自転車で訪れた市町村のみを塗りつぶすプログラムを作った

はじめに

自分は自転車でツーリングで行った後は 思い出にふけるために白地図に対して通った市町村などをポチポチ塗りつぶしたりしてニヤニヤしたりしてました。

↓ ポチポチしてたときに使ったサイト

n.freemap.jp

↓ ニヤニヤしてたときのツイート

Strava APIを使ってツーリングのデータを取り出せるのでこれも自動化できそうだなって思ってプログラムを作ってみました。

何を使うか

最初はGoogle Chart APIというデータを図にしたりできるAPIの一つであるGoogle GeoChartを使おうと考えました。

Google GeoChartは日本地図に対して色を塗ったりできますが、塗りつぶしの最小単位が都道府県で、 市町村を塗りつぶすという要件は満たしませんでした。

更に調べていくとD3.jsというJavaScriptのパッケージを使って日本地図を描画している人がちらほらいました。

hiyuzawa.jp

qiita.com

記事も充実してやりやすそうだと思い今回はD3.jsを使うことにしました。

D3.jsとは

D3.jsはデータを視覚化したりすることに使われることが多いですが、D3.js自体に描画機能はなく JSONやCSVなどによって与えたデータから描画位置などを計算したり、その描画位置などのデータを付加してDOM操作ができるライブラリです*1。

描画自体はHTML,CSS,SVGなどのWeb標準の機能に準拠します。

d3js.org

D3.jsには緯度経度から描画用のピクセル座標に変換するメソッドなどもあり、今回はそのあたりのメソッドをメインに使っていきます。

D3.jsで白抜き地図を出力してみる

D3.jsを使って白抜きの地図を出力してみます。そのためには元となる地図データが必要です。

地図データの取得

今回の地図データはROIS-DS人文学オープンデータ共同利用センターが提供している市区町村及び行政区毎に境界線が引いてある北海道の地図データを使用します。

geoshape.ex.nii.ac.jp

↑を見るとどのような地図データなのかのプレビューが見られます。

複数の年月日で地図データがおいてあります。 一番古い1920-01-01と最新の2021-01-01を見比べると市町村の合併などで行政区の境界線が変わっていることがわかります。 今回は最新の2021-01-01を使います。

各年月日でも解像度毎にデータセットが分かれています。あまりにも大きい解像度のデータを使うとこの後の変換処理などが重くなるので、今回は中解像度を使います。

ダウンロードしたファイルの形式がtopojsonというテキストファイルになっています。 この形式のデータを加工してD3.jsでマッピングできる形に持っていきます。

TopoJSONとGeoJsonとは

ダウンロードしたtopojsonという形式のファイルはGISデータを表現できるTopoJSONという規格で保存されたファイルです。 同じくGISデータを表現するためのGeoJSONという規格から軽量化を考えて作られた規格です。

github.com

TopoJSONを読み込む

ダウンロードしたTopoJSONを読み込みます。 TypeScriptで扱うための型定義があるのでインストールします。

www.npmjs.com

TopoJSONはその名の通り、フォーマットはJSONベースなのでJSONファイルとして読み込めます。 ただし、読み込む際の型はTopology型にします。

import { Topology } from "topojson-specification";

async function main() {
  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );
  console.log(topo);
}

読み込んだtopojsonを出力すると、オブジェクトになっていることがわかります。

SVGを出力する

TopoJSONのデータから地図をSVG形式で表示します。

TopoJSONからGeoJSONに変換する

D3.jsで読み込むためにはTopoJSONからGeoJSONに変換する必要があります。 変換にはtopojson-clientライブラリを使うため型定義と共にインストールします。

www.npmjs.com

www.npmjs.com

topojson-clientのfeatureメソッドでTopoJSONの指定したオブジェクトをGeoJSONに変換することができます。 TopoJSONにはGeometryCollectionという要素があります。

qiita.com

GeometryObjectと呼ばれる点、線、面、ポリゴン、GeometryCollection*2などのデータが集まったものがGeometryCollectionです。

GeoJSONにてGeometryCollectionに対応するのがFeatureCollection、GeometryObjectに対応するのがFeature及びFeatureCollectionです。

featureメソッドの第一引数にはtopojsonそのものを、第二引数にはGeometryObjectを指定します。 返り値は指定したGeometryObjectから変換されたFeatureCollectionまたはFeatureです。

今回のtopojsonはobjects.cityにGeometryCollectionが入っています。 試しに出力してみます。

import { Topology } from "topojson-specification";

async function main() {
  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );
  console.log(topo.objects.city);
}

すると、以下のようなオブジェクトになっているのがわかります。

{
  type: 'GeometryCollection',
  geometries: [
    {
      type: 'MultiPolygon',
      arcs: [Array],
      id: '北海道札幌市中央区',
...

featureメソッドを使ってGeometryCollectionをGeoJSONのFeatureCollectionに変換します。

import * as topojson from "topojson-client";
import { Topology } from "topojson-specification";

async function main() {
  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );
  const geo = topojson.feature(topo, topo.objects.city);
  console.log(geo);
}

これで出力すると

{
  type: 'FeatureCollection',
  features: [
    {
      type: 'Feature',
      id: '北海道札幌市中央区',
      properties: [Object],
      geometry: [Object]
    },
    {
...

変換できていることがわかります。

FeatureCollectionはFeatureの集まりです。D3.jsで変換処理する際はFeatureを一つずつ取り出して処理するためFeatureCollectionからFeatureのIterableな値を取り出す必要があります。

FeatureCollectionが持つfeaturesというプロパティにFeatureの配列が入っています。

つまり、geo.featuresでFeatureの配列として取り出せます。

const features = geo.features

しかし、TypeScriptでは、topojson.featureによって変換した際のgeoの型はFeature | FeatureCollectionとなっています*3。 Feature型だった場合はgeo.featuresというプロパティは存在しません。

Feature型かFeatureCollection型かどうかはgeo.typeにstring型で入っています。

よって、featuresは

const features =
  geo.type === "FeatureCollection"
    ? geo.features
    : geo.type === "Feature"
      ? [geo]
      : undefined;
if (!features) {
  throw new Error();
}

typeの場合分けによって取得できます。

GeoJSONを元にSVGを出力する

SVGはXMLによって記述されています。D3.jsでピクセル座標に変換後はDOM操作でSVGを構築する必要がありますが、 今回はNode.jsを使用しているため、Node.jsでDOM操作ができるJSDOMをインストールします。

www.npmjs.com

JSDOMとD3.jsを使ってGeoJSONからSVGに変換します。

DOM操作するためにJSDOMのインスタンスを生成してdocumentオブジェクトを取得します。

const document = new JSDOM().window.document;

次に緯度経度から特定のピクセル座標に変換する関数をD3.jsで作ります。

import * as d3 from "d3";
...
const aProjection = d3
  .geoMercator()
  .center([center.lng, center.lat])
  .translate([width / 2, height / 2])
  .scale(scale);

geoMercator関数は緯度経度をメルカトル図法の地図にマッピングします。 マッピングする際に以下の情報を与えることでその情報を踏まえてマッピングする関数を返します。

例えば、800x800の画像に5000倍の大きさでSVGを出力したい場合を考えます。

800x800の画像の中心は(400,400)なのでtranslateにはそれを与えます。

5000倍の大きさなのでscaleもそのまま与えます。

centerについて、まずは北海道の地図を出力するので北海道の中心を見つけます。

Google Mapsでだいたい北海道の真ん中あたりに合わせてURLに入っている緯度経度をcenterに与えます。

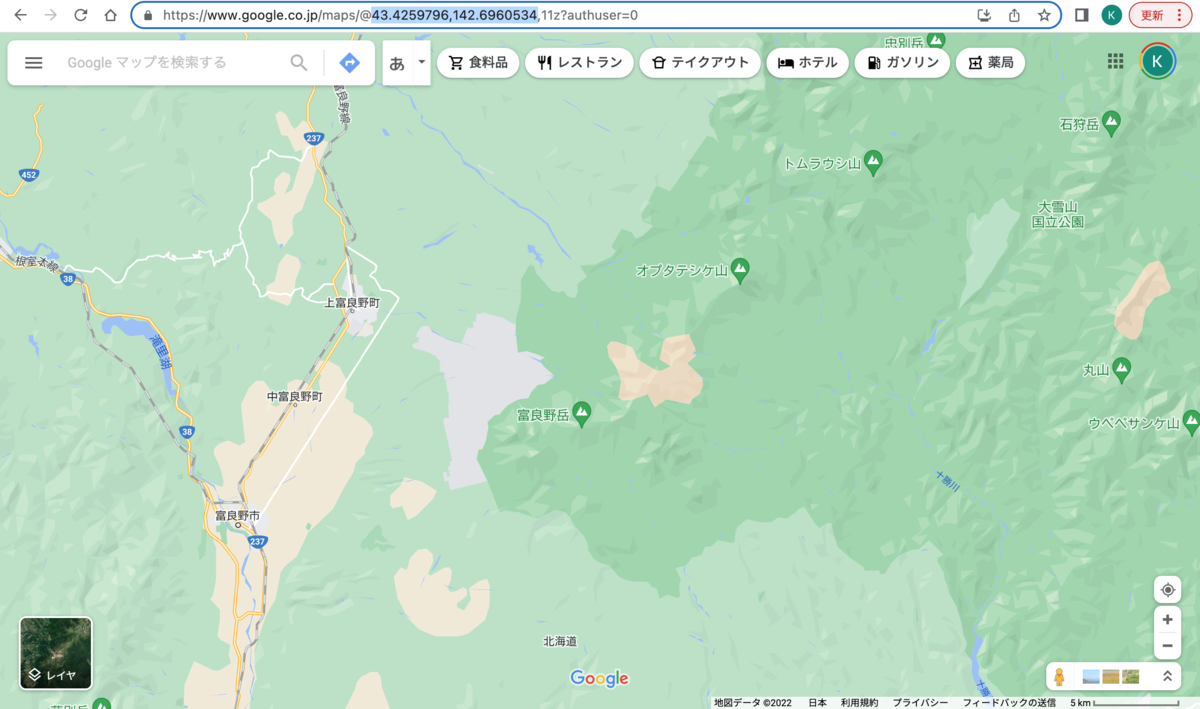
今回の場合は43.4259796,142.6960534です。 コードにすると以下です。

import * as d3 from "d3";
...
const aProjection = d3
  .geoMercator()
  .center([142.6960534, 43.4259796])
  .translate([400, 400)
  .scale(5000);

centerに与える際は経度、緯度の順番です。 Google Mapsに表示されている順番と逆であることに注意してください。

これで緯度経度からピクセル座標に変換するaProjectionという関数を取得できます。

次にD3.jsのgeoPath関数を使って、GeoJSONのFeatureからSVGのフォーマットに変換する関数を取得します。

geoPath().projection() の引数に先程取得したaProjectionを渡すと、FeatureからSVGフォーマットに変換する関数を取得できます。

import * as d3 from "d3";
...
const aProjection = d3
  .geoMercator()
  .center([142.6960534, 43.4259796])
  .translate([400, 400)
  .scale(5000);

const geoPath = d3.geoPath().projection(aProjection);

geoPathという関数を取得しました。

geoPathをGeoJSONのFeature一つ一つに適用していきSVGフォーマットに変換していきます。 また、同時にDOM操作によってSVGを構築していきます。

  const d3Svg = d3
    .select(document.body)
    .append("svg")
    .attr("xmlns", "http://www.w3.org/2000/svg")
    .attr("width", 800)
    .attr("height", 800);

d3.selectでタグを選択できます。bodyの中にSVGを作りたいので、document.bodyを選択します。

appendでタグを追加できます。svgタグを追加します。

更にattrでsvgタグに属性を追加します。svgタグに必要な属性を追加します。

これで、800x800の空のSVGが出来上がります。

elementオブジェクトとしてd3Svgを取得し、GeoJSONのデータを変換しつつ入れていきます。

  d3Svg
    .selectAll("path")
    .data(features)
    .enter()
    .append("path")
    .attr("d", geoPath)
    .style("stroke", "#000000")
    .style("stroke-width", 3)
    .style("fill", "#ffffff");

dataとenterでpathタグの要素にGeoJSONを入れていきます。

selectAllとappendでpathタグをfeaturesの個数だけ生成します。

attrにgeoPath関数を指定して、featuresの中身一つ一つにgeoPath関数を適用した結果をpathの中に入れていきます。

この辺りの挙動は難しく

wizardace.com

ここを参考にしました。

styleでpathタグにスタイルを適用します。SVGの線の色と太さを指定しています。

これらのDOM操作によって、SVGが構築できました。

実際にHTMLを表示してみます。

console.log(document.body.innerHTML);

すると、

<svg xmlns="http://www.w3.org/2000/svg" width="800" height="800"><path d="M376.59773479337764,408.5635356562202L376.6120848716737,408.56283232223666L376.7894585138747,
...
</path></svg>

このようにSVGが出力されます。 ファイルに出力してブラウザなどで開くと市町村の境界線付きで北海道の地図が表示されます。

指定の市町村によって塗りつぶす色を変える

指定した市町村の区域を別の色で塗りつぶしてみます。

今回ダウンロードしたTopoJSONにはGeometry毎に市町村名がついています。

GeoJSONに変換した後にはFeature毎に対応した市町村名が入っています。

{
  type: 'FeatureCollection',
  features: [
    {
      type: 'Feature',
      id: '北海道札幌市中央区',
      properties: [Object],
      geometry: [Object]
    },
    {
...

idとして入っています。

このidをSVGを構築する際のHTMLのpathタグのclass名として利用します。

  d3Svg
    .selectAll("path")
    .data(features)
    .enter()
    .append("path")
    .attr("d", geoPath)
    .attr("class", (d) => {
      return d.id ? d.id : "unknown";
    })
    .style("stroke", "#000000")
    .style("stroke-width", 1)
    .style("fill", "#ffffff");

pathタグに classという属性を指定します。attrの第二引数に関数を指定できます。

ここに指定した関数の引数であるdはfeaturesから取り出されたデータです。つまりFeatureです。

今回はclass名に市町村名を使うためidを取り出して返す関数をattrの第二引数に指定します。

これで各pathタグに市町村名のclassが付与されました。 selectを使ってCSSセレクタで特定のクラスを指定します。

今回は北海道北見市を青色に塗りつぶしてみます。

d3Svg.select(".北海道北見市").style("fill", "blue");

これで北見市を塗りつぶせます。

出力すると

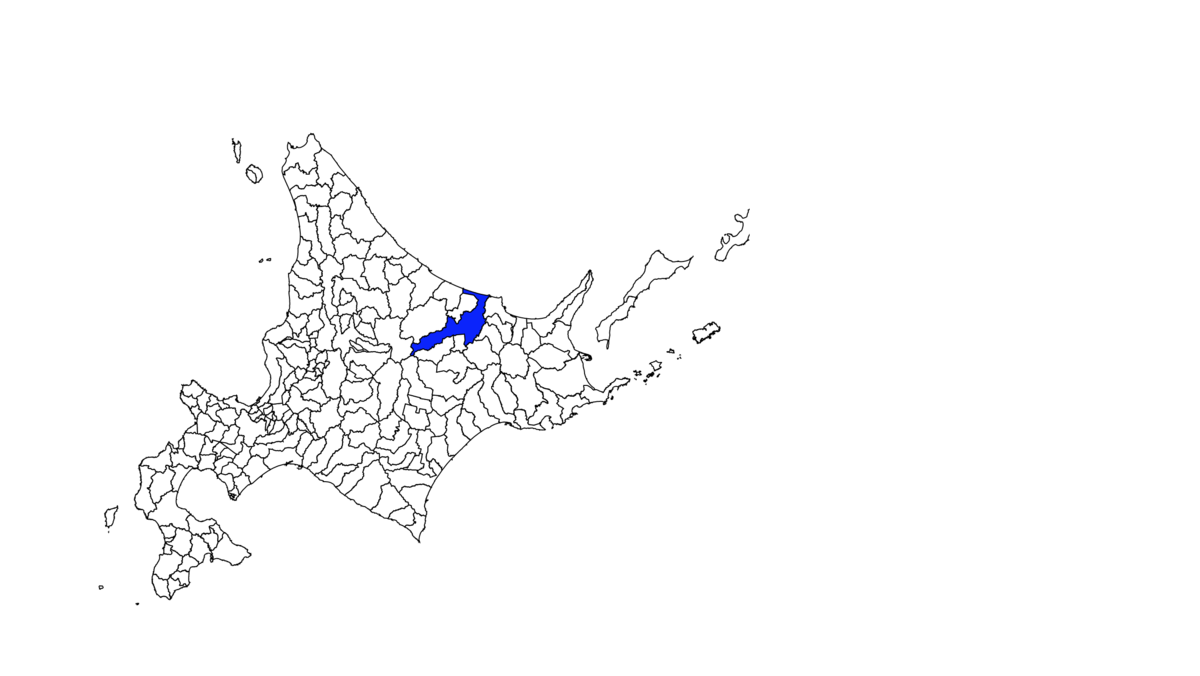
北見市が青色に塗りつぶされていることがわかります。

d3Svg.select(".北海道北見市").style("fill", "blue");
d3Svg.select(".北海道宗谷郡猿払村").style("fill", "red");
d3Svg.select(".北海道雨竜郡幌加内町").style("fill", "yellow");
d3Svg.select(".北海道釧路市").style("fill", "green");

複数塗りつぶすことも可能です。

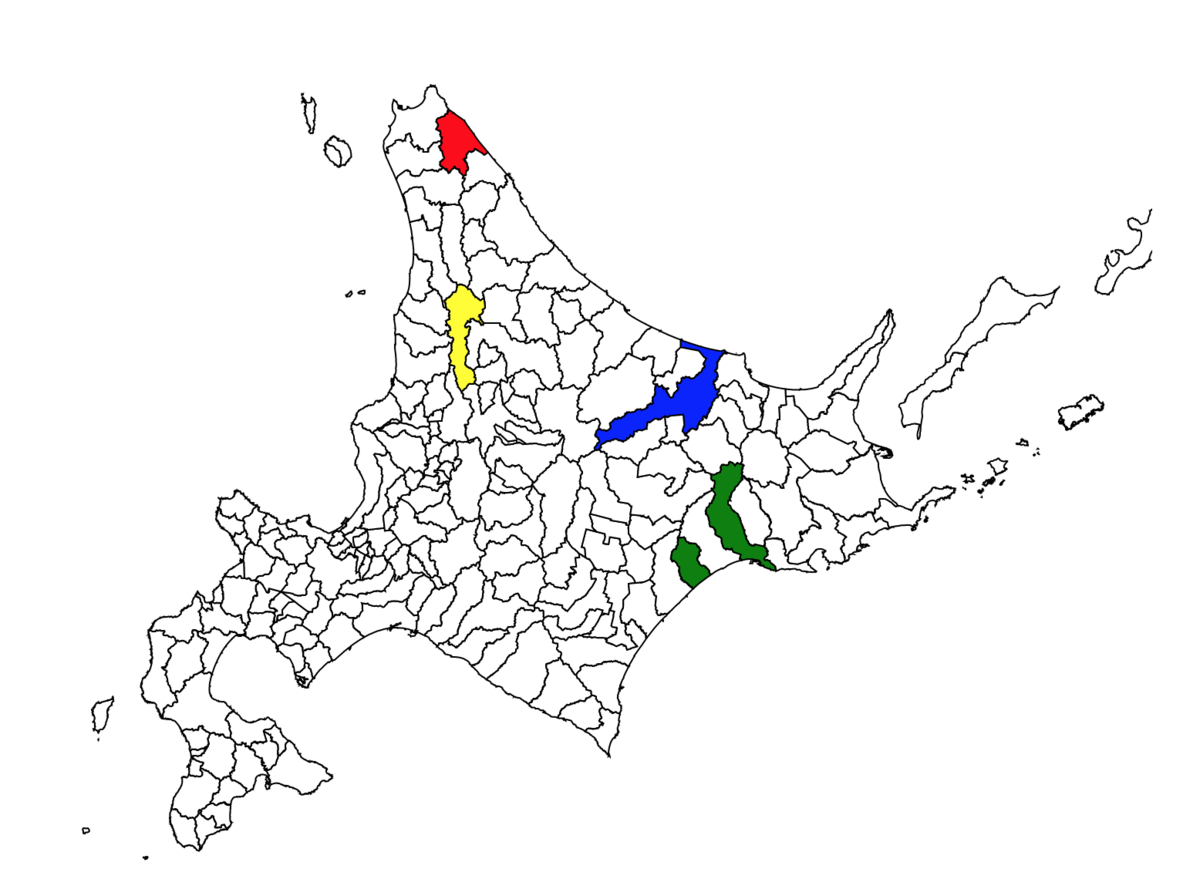
飛び地の釧路市もちゃんと塗りつぶせてます。

StravaのGPSデータから訪問した市町村を取り出して塗りつぶす色を変える

次はStravaのGPSデータから訪問した市町村を取り出して塗りつぶす方法を考えます。

Stravaのデータの取得方法やどのようなデータが入っているかは

muscle-keisuke.hatenablog.com

を見てください。

Stravaのデータから得られる位置情報は緯度経度のみです。特定の緯度経度がどの市町村なのかを取得する必要があります。

geoloniaさんが出している緯度経度から市町村を取り出すOSSがあるのでこちらを利用させてもらいます。

github.com

インストールして使ってみます。緯度経度から室蘭工業大学がどこの市町村にあるかを取得してみます。

室蘭工業大学の緯度経度は42.3785905,141.0373005なので

import { openReverseGeocoder } from "@geolonia/open-reverse-geocoder";

async function main() {
  const res = await openReverseGeocoder([141.0373005, 42.3785905]);
  console.log(res);
}

とすれば取得できます。ここでも緯度経度の順番がGoogle Mapsと関数に渡す順番が違うことに注意してください。

出力は

{ code: '01205', prefecture: '北海道', city: '室蘭市' }

です。室蘭工業大学が室蘭市にあることがわかりました。

これでStravaの位置情報を入れることでどこの市町村を通ったかがわかるようになりました。

今回は今年のGWに北海道をツーリングしたときに走ったある1日のデータを使ってみます。

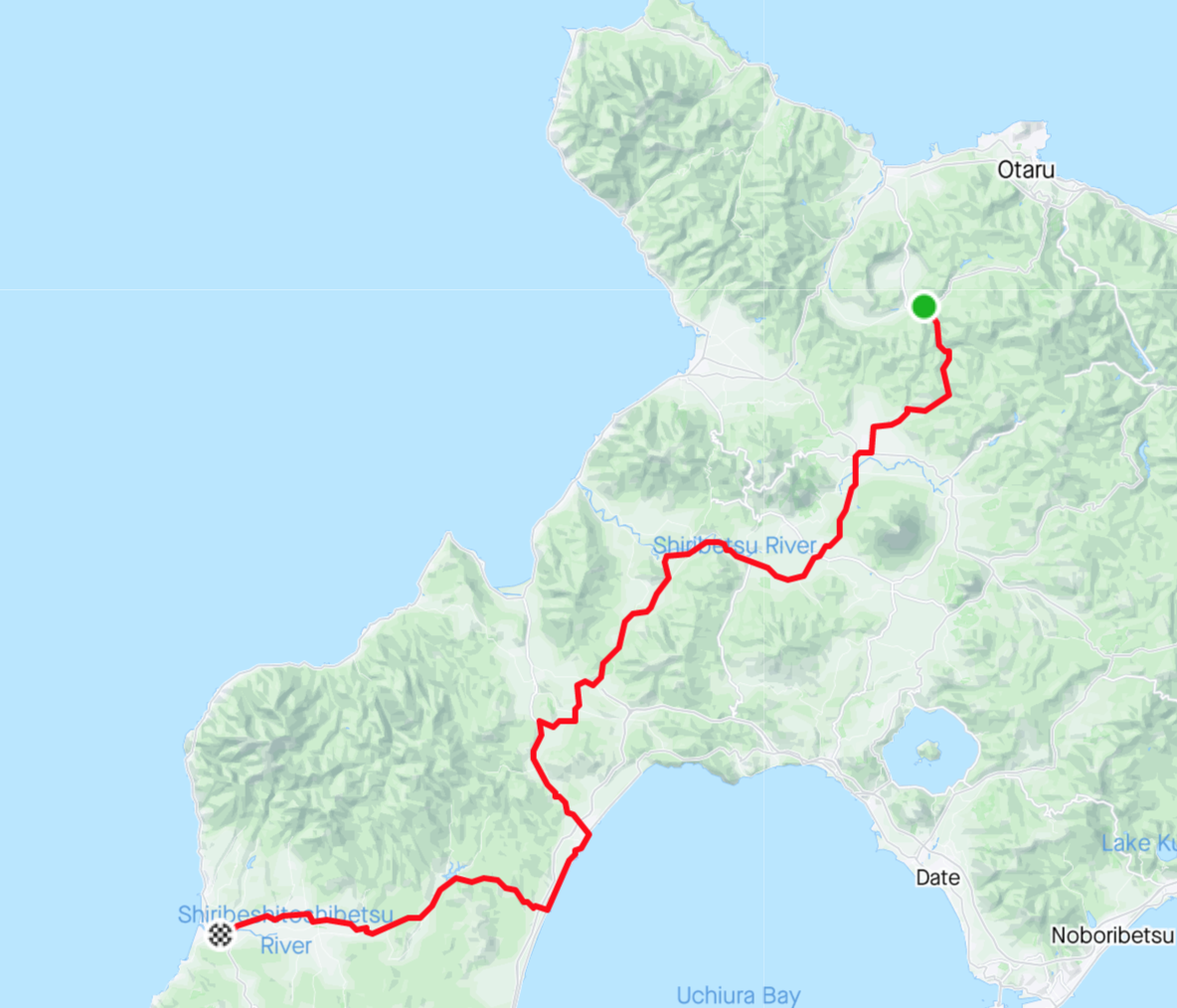
ちなみにこの日は赤井川村からせたな町まで走りました。

あらかじめAPIで取得していたこの日のデータをJSONに保存していたので、これを読み込んで位置情報データを出力してみます。

async function main() {
  const activity = JSON.parse(
    fs.readFileSync("./json/activity.json", "utf-8")
  );
  console.log(activity.map.summary_polyline);

すると、

wqweGksszYtKUdRoa@hGqGhCsUrG...EdKjAxRhPvS_@~LsPbV

文字列が返ってきます。これは位置情報を文字列にして表したPolyline Encodingと呼ばれるものです。 詳しくは過去の記事に載っています。

muscle-keisuke.hatenablog.com

このPolyline Encodingされた位置情報を緯度経度の位置情報に変換する必要があります。 これも変換できるOSSがあるので利用させてもらいます。

github.com

インストールして使います。

import polyline from "@mapbox/polyline";

async function main() {
  const activity = JSON.parse(
    fs.readFileSync("./json/activity.json", "utf-8")
  );

  const positions = polyline.decode(activity.map.summary_polyline);

  console.log(positions);
}

出力すると

[
  [ 43.05196, 140.84422 ], [ 43.04993, 140.84433 ], [ 43.04686, 140.84985 ],
  [ 43.04553, 140.85122 ], [ 43.04484, 140.85484 ], [ 43.04346, 140.85771 ],
  [ 43.04133, 140.85959 ], [ 43.03861, 140.86008 ], [ 43.03689, 140.86253 ],
  [ 43.03551, 140.8635 ],  [ 43.02964, 140.86588 ], [ 43.02341, 140.86626 ],
  [ 43.02118, 140.86784 ], [ 43.01437, 140.86788 ], [ 43.01134, 140.86901 ],
...

緯度経度の配列が取得できました。

一つずつ市町村を取得する関数に通します。

async function main() {
  const activity = JSON.parse(
    fs.readFileSync("./json/activity.json", "utf-8")
  );

  const positions = polyline.decode(activity.map.summary_polyline);

  const regions = await Promise.all(
    positions.map(async (p) => await openReverseGeocoder([p[1], p[0]]))
  );

  console.log(regions);

すると、

[
  { code: '01409', prefecture: '北海道', city: '余市郡赤井川村' },
  { code: '01409', prefecture: '北海道', city: '余市郡赤井川村' },
  { code: '01409', prefecture: '北海道', city: '余市郡赤井川村' },
  { code: '01409', prefecture: '北海道', city: '余市郡赤井川村' },
  { code: '01409', prefecture: '北海道', city: '余市郡赤井川村' },
... 
  { code: '01400', prefecture: '北海道', city: '虻田郡倶知安町' },
  { code: '01400', prefecture: '北海道', city: '虻田郡倶知安町' },
  { code: '01400', prefecture: '北海道', city: '虻田郡倶知安町' },
  { code: '01395', prefecture: '北海道', city: '虻田郡ニセコ町' },
  { code: '01395', prefecture: '北海道', city: '虻田郡ニセコ町' },
  { code: '01395', prefecture: '北海道', city: '虻田郡ニセコ町' },
...
  { code: '01394', prefecture: '北海道', city: '磯谷郡蘭越町' },
  { code: '01394', prefecture: '北海道', city: '磯谷郡蘭越町' },
  { code: '01394', prefecture: '北海道', city: '磯谷郡蘭越町' },
  { code: '01394', prefecture: '北海道', city: '磯谷郡蘭越町' },
  { code: '01394', prefecture: '北海道', city: '磯谷郡蘭越町' },

取得できましたが、一つ一つの緯度経度に対して、市町村を返してしまうので、重複があります。 重複を排除します。

また、codeは必要なくprefectureとcityは一つの文字列に結合してしまっても問題ないのでその処理も合わせて行います。

async function main() {
  const activity = JSON.parse(
    fs.readFileSync("./json/activity.json", "utf-8")
  );

  const positions = polyline.decode(activity.map.summary_polyline);

  const regions = await Promise.all(
    positions.map(async (p) => {
      const res = await openReverseGeocoder([p[1], p[0]]);
      return res.prefecture + res.city;
    })
  );

  const distinctRegions = [...new Set(regions)];

  console.log(distinctRegions);

出力すると

[
  '北海道余市郡赤井川村',
  '北海道虻田郡倶知安町',
  '北海道虻田郡ニセコ町',
  '北海道磯谷郡蘭越町',
  '北海道寿都郡黒松内町',
  '北海道山越郡長万部町',
  '北海道瀬棚郡今金町',
  '北海道久遠郡せたな町'
]

重複を削除して必要な形でデータを取得することができました。

あとは前のセクションで説明した塗りつぶしのコードと組み合わせれば、GPSのデータから訪問した市町村を塗りつぶした地図を出力することができます。

import { Topology } from "topojson-specification";
import * as topojson from "topojson-client";
import * as d3 from "d3";
import { JSDOM } from "jsdom";
import fs from "fs";
import { openReverseGeocoder } from "@geolonia/open-reverse-geocoder";
import polyline from "@mapbox/polyline";

async function main() {
  const document = new JSDOM().window.document;
  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );
  const geo = topojson.feature(topo, topo.objects.city);

  const features =
    geo.type === "FeatureCollection"
      ? geo.features
      : geo.type === "Feature"
        ? [geo]
        : undefined;
  if (!features) {
    throw new Error();
  }

  const aProjection = d3
    .geoMercator()
    .center([142.6960534, 43.4259796])
    .translate([400, 400])
    .scale(5000);
  const geoPath = d3.geoPath().projection(aProjection);
  const d3Svg = d3
    .select(document.body)
    .append("svg")
    .attr("xmlns", "http://www.w3.org/2000/svg")
    .attr("width", 800)
    .attr("height", 800);

  d3Svg
    .selectAll("path")
    .data(features)
    .enter()
    .append("path")
    .attr("d", geoPath)
    .attr("class", (d) => {
      return d.id ? d.id : "unknown";
    })
    .style("stroke", "#000000")
    .style("stroke-width", 1)
    .style("fill", "#ffffff");

  const activity = JSON.parse(
    fs.readFileSync("./json/activity.json", "utf-8")
  );

  const positions = polyline.decode(activity.map.summary_polyline);

  const regions = await Promise.all(
    positions.map(async (p) => {
      const res = await openReverseGeocoder([p[1], p[0]]);
      return res.prefecture + res.city;
    })
  );

  const distinctRegions = [...new Set(regions)];

  for (const region of distinctRegions) {
    d3Svg.select(`.${region}`).style("fill", "#5EAFC6");
  }

  fs.writeFileSync("./hoge.svg", document.body.innerHTML);

出力されたSVGを見てみます。

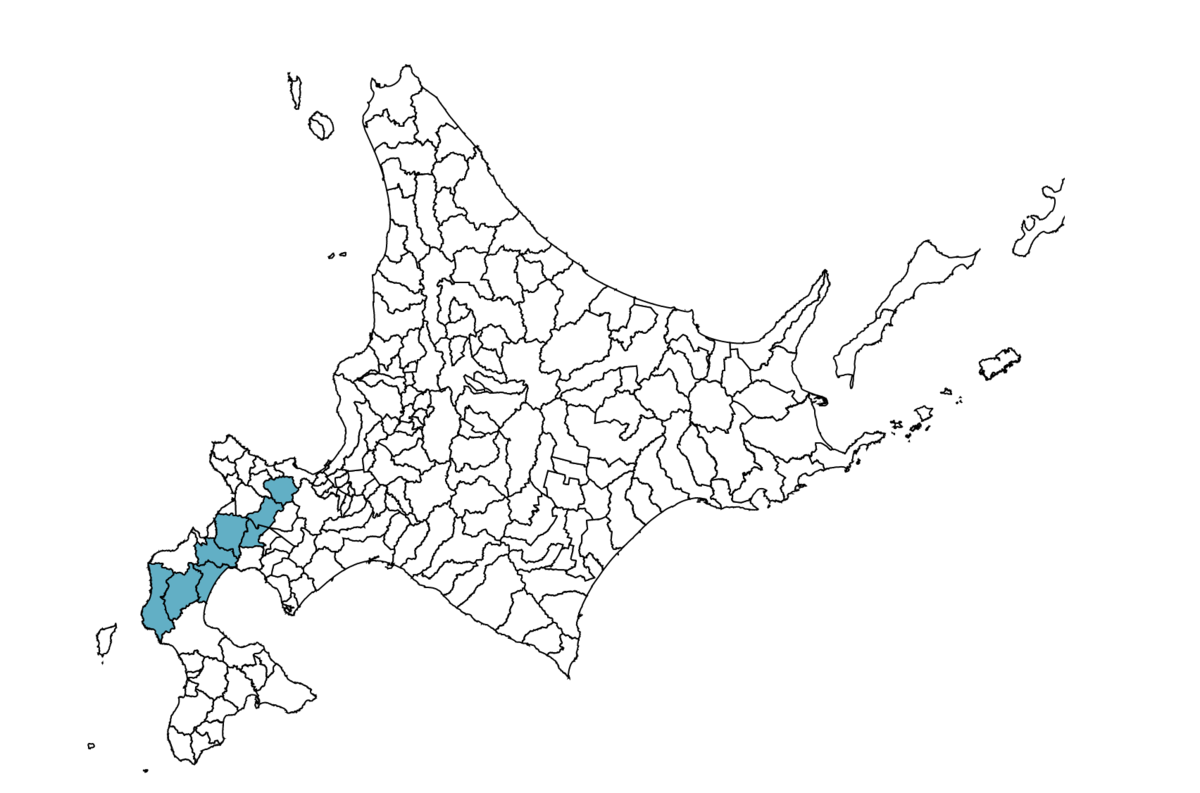
GPS通りの市町村が塗りつぶされています。

中心の緯度経度をTopoJSONから算出する

緯度経度からピクセル座標に変換する際の中心はGoogle Mapsで大体の中心を調べて手入力してました。

  const aProjection = d3
    .geoMercator()
    .center([142.6960534, 43.4259796])
    .translate([400, 400])
    .scale(5000);

これをTopoJSONから算出します。TopoJSONの中にはbboxというプロパティがあります。今回使用しているTopoJSONの場合は

{"type":"Topology","id":"x0401:01","metadata":{"type":["行政区境界"],"dc:title":"北海道 市区町村:中解像度TopoJSON","dc:source":"N03-21_01_210101.shp","dc:issued":"2021-01-01",..."bbox":[139.33396016902668,41.351645558995415,148.89440319085463,45.55724341395245],
...

このように入っています。 取り出すときは

  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );
  console.log(topo.bbox);

これで取り出せます。取り出した値を出力すると

[
  139.33396016902668,
  41.351645558995415,
  148.89440319085463,
  45.55724341395245
]

緯度経度のペア2つが出力されます。この緯度経度は今回使用している北海道のTopoJSONのバウンディングボックスです。

e-words.jp

北海道の南西端の緯度経度と北東端の緯度経度が入っています。

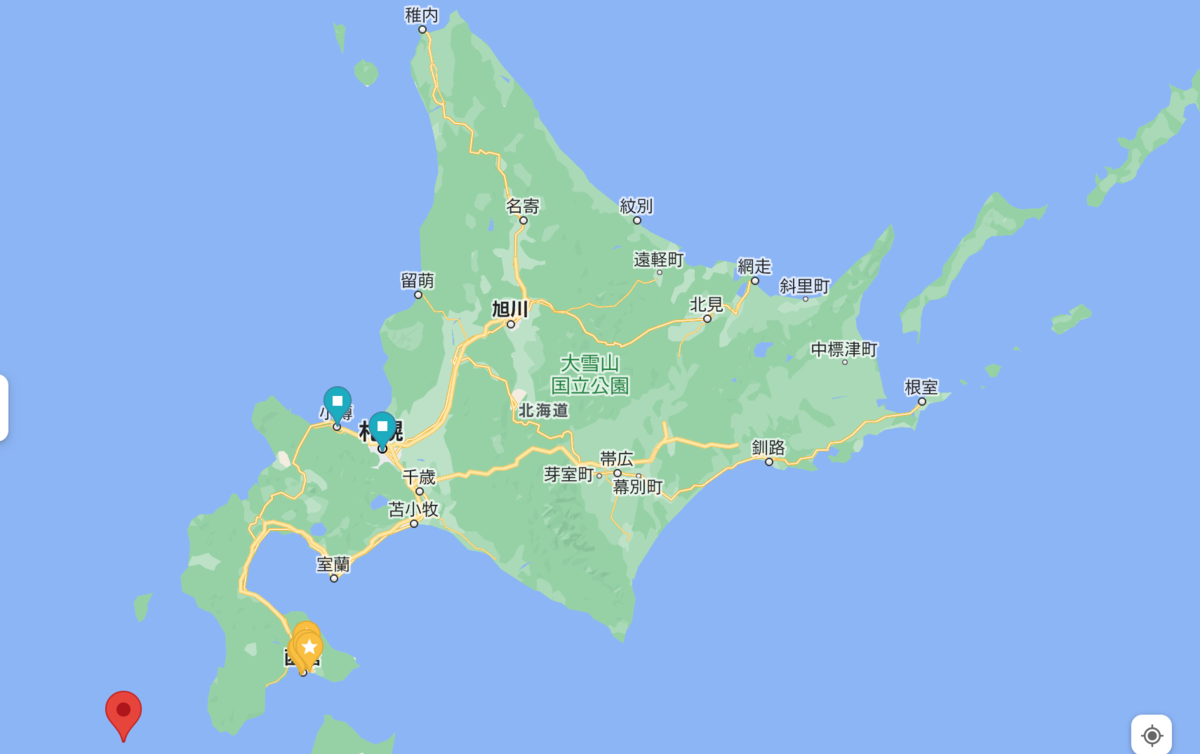
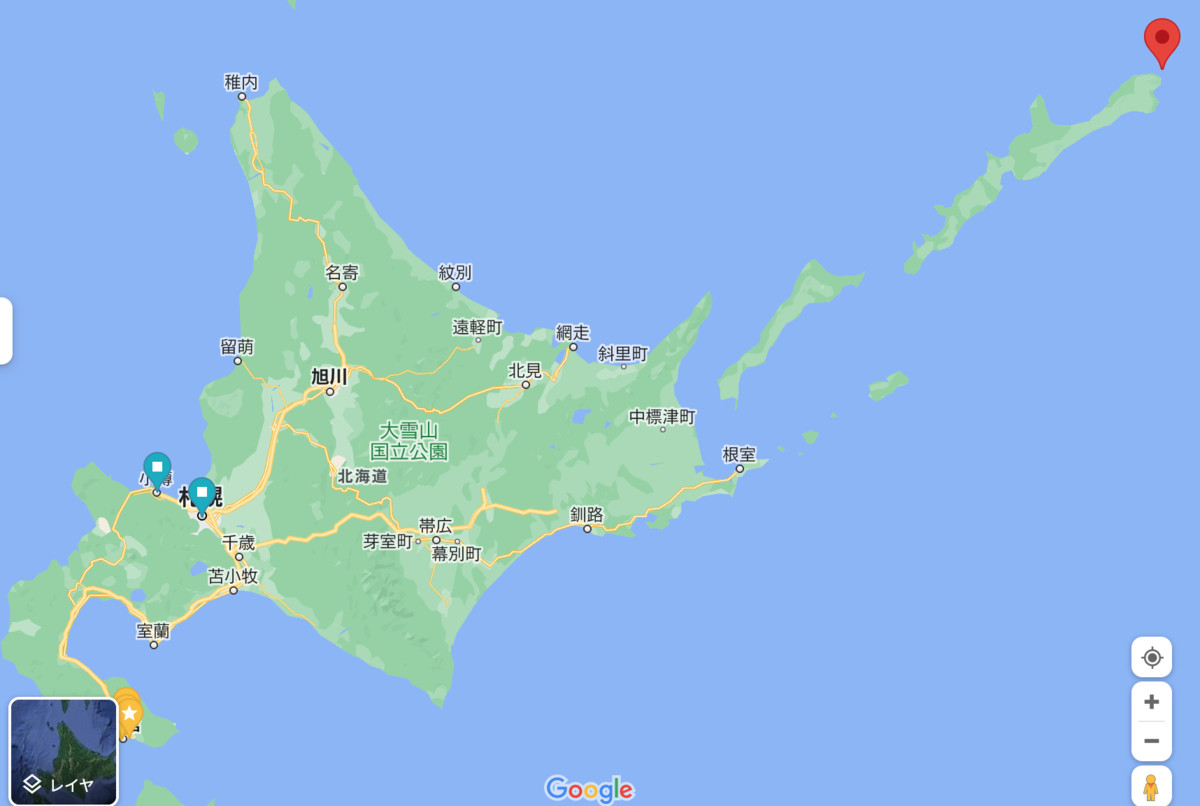
Google Mapsで出力してみると端と端であることがわかります。

これを利用して中心の緯度経度を求めます。

2点間の緯度経度から中間点を求める方法を解説しているサイトがあります。

tma.main.jp

地球を半径1の球体と考えて緯度経度を極座標として考えます。

詳しい導出方法は元のサイトに書いてあるのでここには書かないですが、手順としては

  • 2点の緯度経度をそれぞれ直交座標に変換する
  • 変換した直交座標の中間点を求める
  • 中間点を緯度経度に変換する

です。

まずは2点の緯度経度を直交座標に変換します。

import { Topology } from "topojson-specification";

async function main() {
  const topo: Topology = JSON.parse(
    fs.readFileSync("./topojson/01_city.i.topojson", "utf-8")
  );

  if (!topo.bbox) {
    throw new Error();
  }

  console.log(latLngToPixels({ lat: topo.bbox[1], lng: topo.bbox[0] }));
  console.log(latLngToPixels({ lat: topo.bbox[3], lng: topo.bbox[2] }));
}

function latLngToPixels(arg: { lat: number; lng: number }) {
  const [radLat, radLng] = [degreeToRadian(arg.lat), degreeToRadian(arg.lng)];
  return {
    x: Math.cos(radLng) * Math.cos(radLat),
    y: Math.cos(radLat) * Math.sin(radLng),
    z: Math.sin(radLat),
  };
}

function degreeToRadian(degree: number) {
  return degree * (Math.PI / 180);
}

Mathの三角関数はラジアンを引数に取るので、変換しています。

結果は

{
  x: -0.5693979186700274,
  y: 0.48917259406333097,
  z: 0.6606785780026414
}
{
  x: -0.5995197259339476,
  y: 0.36173329843931645,
  z: 0.7139503617313299
}

です。

これの中間点を求めます。

const aPixels = latLngToPixels({ lat: topo.bbox[1], lng: topo.bbox[0] });
const bPixels = latLngToPixels({ lat: topo.bbox[3], lng: topo.bbox[2] });
// 正規化するので1/2する必要なし
const midPixels = {
  x: aPixels.x + bPixels.x,
  y: aPixels.y + bPixels.y,
  z: aPixels.z + bPixels.z,
};
const midVectorLength = Math.sqrt(
  midPixels.x ** 2 + midPixels.y ** 2 + midPixels.z ** 2
);
const normalizedMidPixels = {
  x: midPixels.x / midVectorLength,
  y: midPixels.y / midVectorLength,
  z: midPixels.z / midVectorLength,
};
console.log(normalizedMidPixels);

出力すると中間点の直交座標が求まります。

{
  x: -0.5859244396192019,
  y: 0.4265198327143081,
  z: 0.6890380129994881
}

求めた中間点の直交座標を緯度経度に戻します。

...
  const midLat = radianToDegree(Math.asin(normalizedMidPixels.z));
  const midLng = radianToDegree(
    Math.atan2(normalizedMidPixels.y, normalizedMidPixels.x)
  );

  console.log({ midLat, midLng });
}
...
function radianToDegree(radian: number) {
  return (radian * 180) / Math.PI;
}

直交座標は三角関数で求めたので緯度経度に戻すときは逆三角関数を使います。

出力は

{ midLat: 43.55400742272156, midLng: 143.94750122681177 }

これをGoogle Mapsで見てみると、

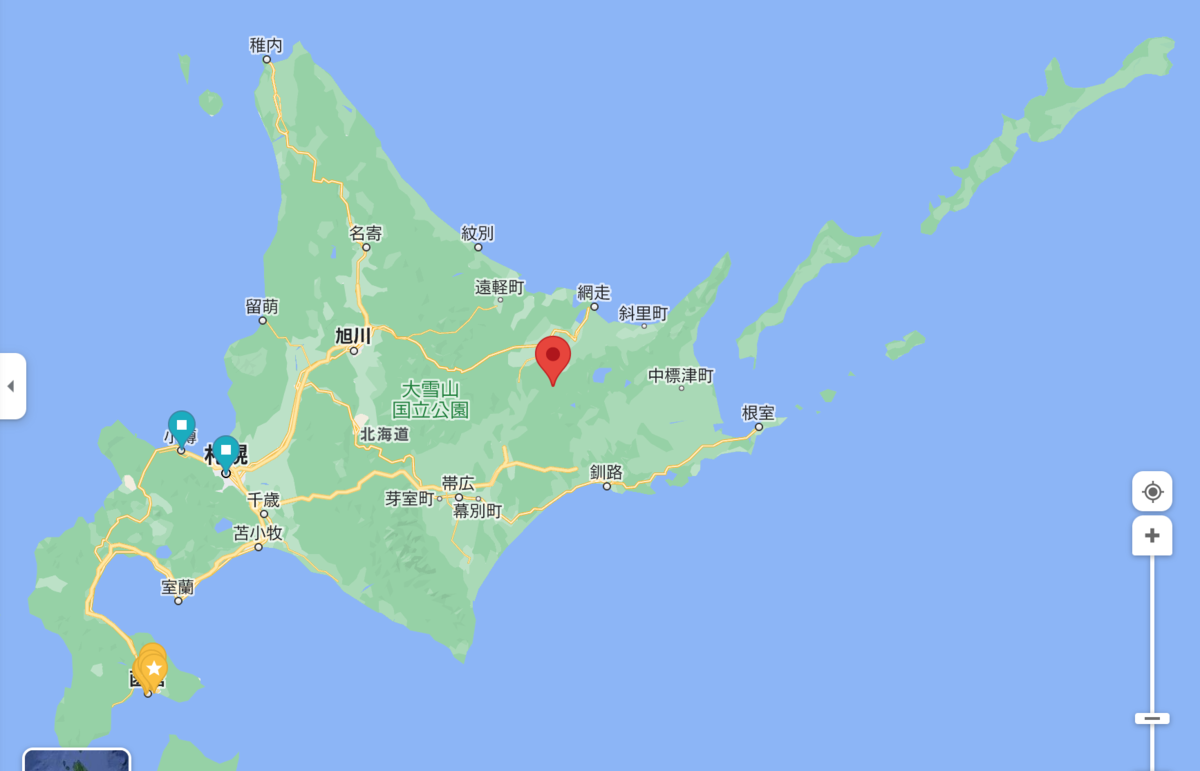
北方四島を含めると確かに中心に見えます。

求めた中心点をD3.jsに入れてSVG出力してみます。

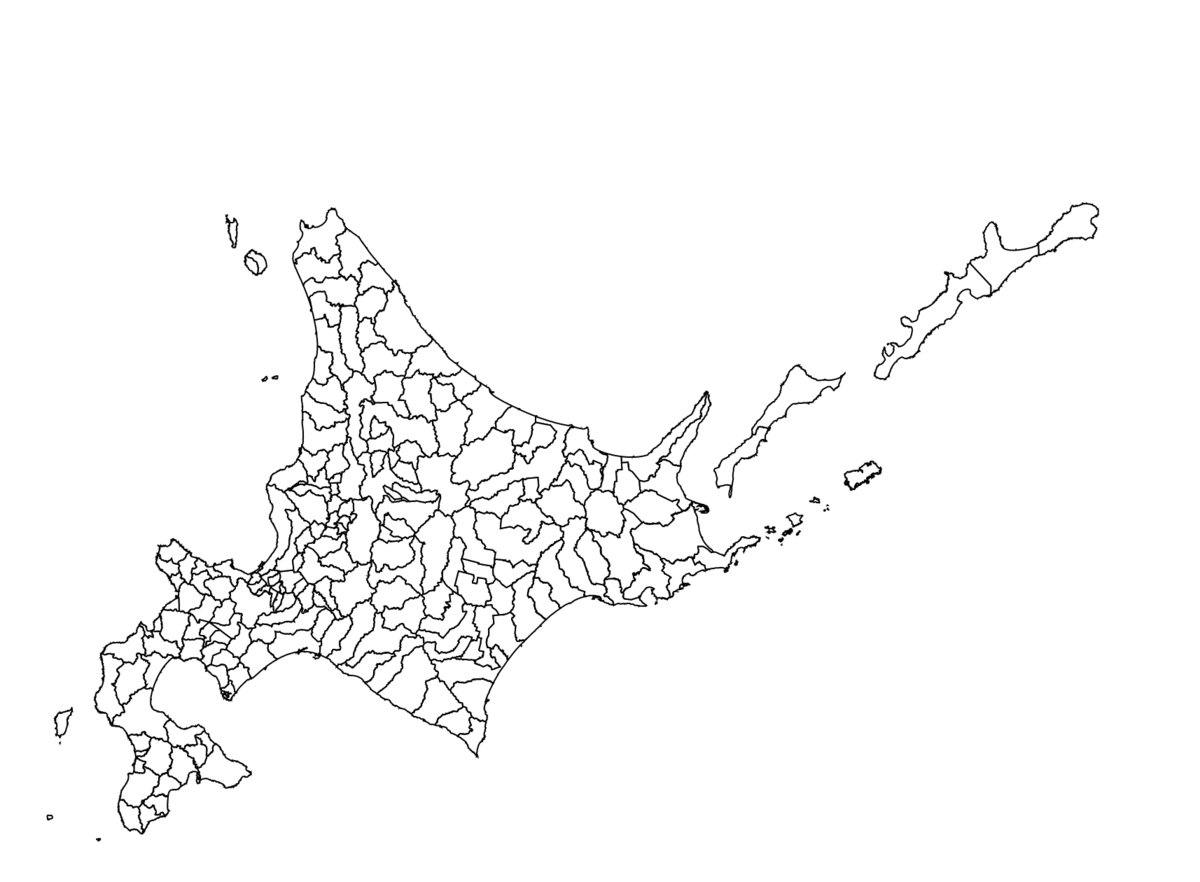
北方四島含めいバランスよく出力されています。

描画範囲全体がバランスよく出力される倍率を求める

D3.jsに指定するscaleも目視で確認して5000倍という値を入れていますが、これもバウンディングボックスを利用して求めることができます。

800x800のSVGを出力することを考えます。

const width = 800;
const height = 800;

const originProjection = d3.geoMercator().scale(1);

const minPosition = originProjection([bbox[0], bbox[1]]) ?? [0, 0];
const maxPosition = originProjection([bbox[2], bbox[3]]) ?? [0, 0];

const originWidth = Math.abs(maxPosition[0] - minPosition[0]);
const originHeight = Math.abs(maxPosition[1] - minPosition[1]);

const scale = Math.min(width / originWidth, height / originHeight);

まず1倍でメルカトル図法で緯度経度をピクセル座標にマッピングする関数を作ります。

const width = 800;
const height = 800;

const originProjection = d3.geoMercator().scale(1);

そして、バウンディングボックスの2点をピクセル座標に変換します。

const minPosition = originProjection([bbox[0], bbox[1]]) ?? [0, 0];
const maxPosition = originProjection([bbox[2], bbox[3]]) ?? [0, 0];

倍率1倍における端の座標が求まります。端2点のwidthとheightを差から求めます。

const originWidth = Math.abs(maxPosition[0] - minPosition[0]);
const originHeight = Math.abs(maxPosition[1] - minPosition[1]);

必要なSVGの長さは800x800なので、originWidthとoriginHeightの何倍に当たるかを求めます。 これが倍率です。

ただし、倍率そのままだと余白がない状態なので求めたscaleを95%にします。 また、元のバウンディングボックスが縦と横で大きさが異なるため、求まる倍率も異なります。

倍率が大きい方に合わせると当然描画範囲をはみ出るのでMath.minで小さい方を取得します。

const scale = 0.95 * Math.min(width / originWidth, height / originHeight);

北海道は北方四島の分があり、縦よりも横に長くなるため、倍率は横の方が小さくなります。

求めたscaleを使ってSVGを出力してみます。

const aProjection = d3
  .geoMercator()
  .center([midLng, midLat])
  .translate([width / 2, height / 2])
  .scale(scale);

全体がバランス良く出力されています。

SVGからPNGに変換する

Twitterに載せたりするために、SVGからPNGに変換します。 Node.jsで画像処理できるsharpを使ってみます。

www.npmjs.com

型定義も入れます。

www.npmjs.com

出力したSVGファイルに対して、変換を行います。

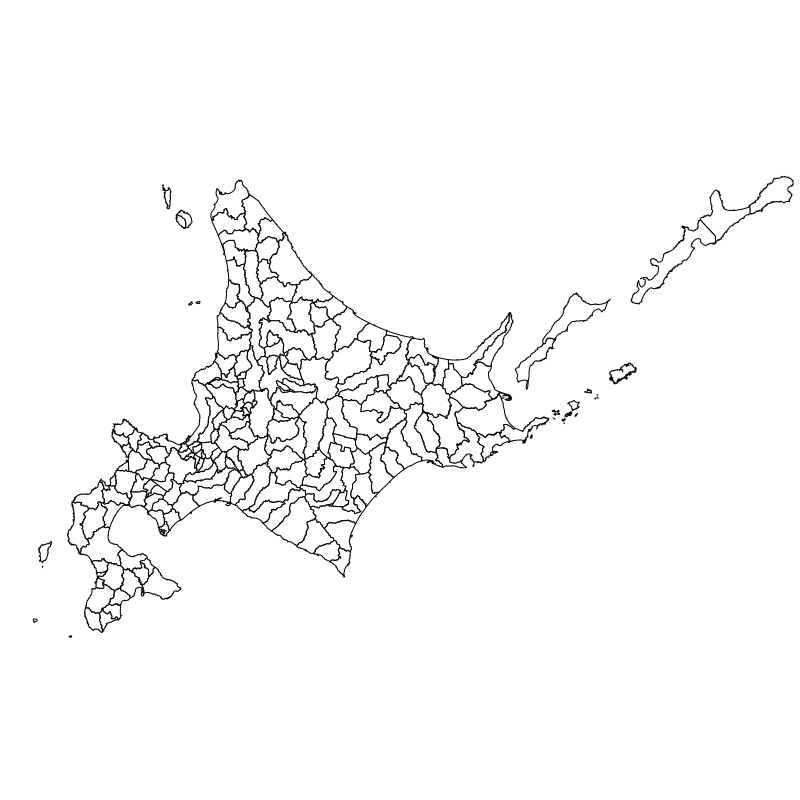
import sharp from "sharp";

async function main() {
...
  fs.writeFileSync("./hoge.svg", document.body.innerHTML);

  await sharp("./hoge.svg").png().toFile("./hoge.png");
}

800x800のPNG画像が出力されました。

*1:D3.jsはData-Driven-Documentsから名付けられている

*2:GeometryCollectionの入れ子がありえる

*3:featureメソッドにはGeometryObjectが引数として渡るため

Google Maps Static APIを使ってツーリングで巡ったルートを地図表示する

はじめに

前回、StravaのAPIを使ってサイクリングの情報を持ってくる方法を記事にしました。

muscle-keisuke.hatenablog.com

Stravaにはどこを走ったかも記録されていて、位置情報が以下のように地図に表示されています。

ちなみにこれは去年今年に北海道で年越しツーリングして大晦日に吹雪に遭ったときのアクティビティです。

遠軽町から湧別町を時速4kmくらいで移動しました。

そのアクティビティをAPIで取得すると位置情報は以下のフォーマットで取得されます。

なんのこっちゃって感じですね。

Strava APIから取得した位置情報もこうなっては人間が読めないので地図画像として出力する必要があります。

今回はGoogle Map Static APIを使ってこの呪文みたいな文字列からStravaに表示されるような地図を生成します。

Google Maps Static APIとは

Google Mapの一部を画像として切り出して返してくれるAPIです。

あらゆる情報をパラメータとして指定することで追加の情報を付加した地図も返せます。

developers.google.com

今回は位置情報を付加した地図を返します。

APIキー取得まで

プロジェクトの作成

developers.google.com

まずは前提として、Googleアカウントが必要です。持っていない場合はアカウントを作成してください。

Googleにログインした後は、プロジェクトを作成します。 Google Cloud Platformにアクセスします。

console.cloud.google.com

右上の「プロジェクトを作成する」から新規のプロジェクトを作成します。

自分がわかるような名前を付けます。

作成後は作成したプロジェクトの画面に遷移します。

支払情報の登録

APIの使用は従量課金制です。APIを使用する前にプロジェクトに支払い方法を登録する必要があります。

Google Maps Static APIの料金

developers.google.com

APIのリクエスト1回毎に0.02USDかかる計算です。

しかし、

developers.google.com

なお、すべての Google Maps Platform ユーザーは、課金が有効になっているアカウントで、毎月 200 ドルのクレジットを受け取ります。

とあるので、2022年6月16日現在はGoogle Maps Static APIのみの利用に限れば、月に10000回までは無料でAPIを叩けます。

それ以上使う場合はプロジェクトに登録された支払い方法によって、従量課金が発生します。

プロジェクトに支払情報を登録する

Google Cloud Platformトップに戻ってサイドバーの「お支払い」を押す。

「請求先アカウントをリンク」を押す。

「請求先アカウントを作成する」を押す。

ここから請求先を登録していきます。まずは必要事項を入力して利用規約を読んで同意します。

プロジェクトのニーズは自分の場合は「個人的なプロジェクト」にしました。

連絡先を確認します。SMSを受信できる電話番号を入力します。

コードを送信すると、入力した電話番号宛にSMSが届きます。

SMSの中に記載されているコードを入力します。

次にお支払い情報の入力です。有効なクレジットカードの情報と住所を入力します。

これで登録は完了です。再度、お支払いのページを見ると、紐付いている請求先アカウントの情報が表示されます。

APIを有効化する

使用するAPIを選びます。 左のサイドバーから「APIとサービス」 -> 「有効なAPIとサービス」を選びます。

「APIとサービス」画面が開くので上の「APIとサービスの有効化」を押します。

「APIライブラリ」で有効にしたいAPIを検索します。

Google Maps Static APIを探します。 staticなどで検索するとヒットすると思います。

該当するAPIを選択します。

「有効にする」を押すと、有効になります。

そのまま有効なAPIが表示される画面に遷移します。

次にAPIキーを発行します。 サイドバーから「認証情報」に遷移して上の「認証情報を作成」からAPIキーを選択します。

すると、APIキーが発行されて表示されます。

Google Maps Static APIを使ってみる

APIキーを利用して画像を表示させてみます。 APIのエンドポイントは以下のようなフォーマットです。

https://maps.googleapis.com/maps/api/staticmap?center=[LATITUDE],[LONGTITUDE]&zoom=[ZOOM_LEVEL]&size=[WIDTH]x[HEIGHT]&key=[API_KEY]

クエリパラメータのcenterにある[LATITUDE],[LONGTITUDE]は表示する地図の中心の緯度経度を入力します。

zoomはズームレベルといって地図の縮尺です。 詳細は

muscle-keisuke.hatenablog.com

の「正方形タイルによる地図表現」セクションに載せています。

sizeの[WIDTH]x[HEIGHT]は表示する地図画像のサイズです。

keyの[API_KEY]は先程発行したAPIキーを入力します。

例えば、小田原駅の地図を表示してみます。 Google Mapで小田原駅を真ん中に寄せたときのURLが

https://www.google.co.jp/maps/@35.2562828,139.1554468,17z?hl=ja

です。URL内に緯度経度とズームレベルがあるのでこれを使います。

画像サイズは600x600にしてみます。すると叩くAPIは

https://maps.googleapis.com/maps/api/staticmap?center=35.2564493,139.1532045&zoom=17&size=600x600&key=[API_KEY]

です。APIキーは伏せているので各自のキーに置き換えてください。

GETリクエストなのでブラウザにURL貼って遷移すると、地図画像が表示されました。

Google Mapで見た地図とまんま一緒です。

これでAPIが使えることを確認できました。

署名の導入

今のままでもAPIは使えますが、GoogleはAPIを叩くときにリクエストを署名することを推奨しています。

developers.google.com

We strongly recommend that you use both an API key and digital signature, regardless of your usage.

リクエストにはAPIキーが含まれています。このAPIキーが何かしらの原因で抜き取られた場合は第三者がAPIを叩けてしまいます。 本人だけが持っている情報でリクエストを署名することで第三者が抜き取ったAPIキーだけではAPI叩けないようにして安全性を高めます。

こちらにGoogle Maps Static APIを使うときに署名する理由などが書いてあります。

Google Developers Japan: Google Maps Platform ベストプラクティス：Static Map API と Street View API を使う際の、より安全な API キーの設定方法

ちなみに前回説明した

muscle-keisuke.hatenablog.com

Strava APIはOAuth2.0による認証です。

仕組みなど定義はこちらがわかりやすかったです。

qiita.com

この中の「認可コードフロー」と「リフレッシュトークンフロー」をStrava APIは採用しています。

GoogleのAPIはGoogle DriveのAPIなど個人のデータにアクセスするAPIにはOAuth2.0を採用して、 Google Maps Static APIのような取得する地図データは個人情報にあたらないのでAPIキーによる認証を採用しているようです。

cloud.google.com

署名を試す

URLやパラメータの署名のやり方です。まず、Google Maps Platformに行くと、先程発行したAPIキーともう一つ、URL 署名シークレットというものがあります。

これが署名には必要です。発行されていない場合はボタンを押して発行してください。

発行後、「URL に署名」の欄から試しにURLを署名することができます。先程の小田原駅を表示するURLを署名してみます。

https://maps.googleapis.com/maps/api/staticmap?center=35.2564493,139.1532045&zoom=17&size=600x600&key=[API_KEY]

APIキーも含めてフォームに貼り付けます。

すると、署名済みのURLが返ってきます。

署名前のURLとの違いは最後のクエリパラメータにsignatureが追加されていることです。

https://maps.googleapis.com/maps/api/staticmap?...&key=[API_KEY]&signature=[SIGNATURE]

このsignatureが署名済みであることを示しています。

このsignatureが付加された状態でAPIを叩くときはURL署名シークレットとリクエストURLで署名をしてみて、[SIGNATURE]と一致するかどうかを検証します。

一致した場合正しい署名(=第三者によるリクエストではない)なので通常通りレスポンスとして画像が返ってきます。一致しない場合はエラーを返します。

ちなみに署名に使われる関数は一方向関数で[SIGNATURE]からURL署名シークレットを算出することは難しいです。

署名済みのURLをブラウザに入力してリクエストを送ると、先程と全く同じ画像が出力されるはずです。

署名を実装する

署名を試すことはできましたが、実際APIを使うのはコード中なので、未署名のURLから署名済みのURLを作る実装が必要です。

署名は

  • 署名シークレットをURLセーフのbase64*1から通常のbase64へ変換する
  • 通常のbase64になった署名シークレットをデコードする
  • デコードした署名シークレットをキーとしてリクエストのURLをHMAC-SHA1*2でハッシュ化する
  • ハッシュをURLセーフのbase64に変換する
  • 署名済みとしてsignatureパラメータに↑のbase64のハッシュを渡す

といった流れで行われます。

公式が様々な言語のサンプルコードを出しているのでこれを踏まえて実装していきます。

developers.google.com

現在、開発しているアプリがTypescript + NodeJSなのでNodeJSのサンプルコードからdeprecatedなも部分を改変してTypescriptで書きました。

import crypto from "crypto";
import url from "url";
...
function removeWebSafe(safeEncodedString: string) {
  return safeEncodedString.replace(/-/g, "+").replace(/_/g, "/");
}
function makeWebSafe(encodedString: string) {
  return encodedString.replace(/\+/g, "-").replace(/\//g, "_");
}
function decodeBase64Hash(code: string) {
  return Buffer.from(code, "base64");
}

function encodeBase64Hash(key: Buffer, data: string) {
  return crypto.createHmac("sha1", key).update(data).digest("base64");
}
function async sign(apiPath: string, signatureSecret: string) {
  const uri = new URL(apiPath);
  const safeSecret = this.decodeBase64Hash(
    this.removeWebSafe(signatureSecret)
  );
  const hashedSignature = this.makeWebSafe(
    this.encodeBase64Hash(safeSecret, uri.pathname + uri.search)
  );
  return url.format(uri) + "&signature=" + hashedSignature;
}

API呼び出しの制限

署名によるリクエストを設定したので未署名のリクエストはできないよう設定します。

Google Maps Platformから「割り当て」を選びます。

未署名のURLによるリクエストの設定を展開して、各API呼び出し回数の上限をすべて0にします。

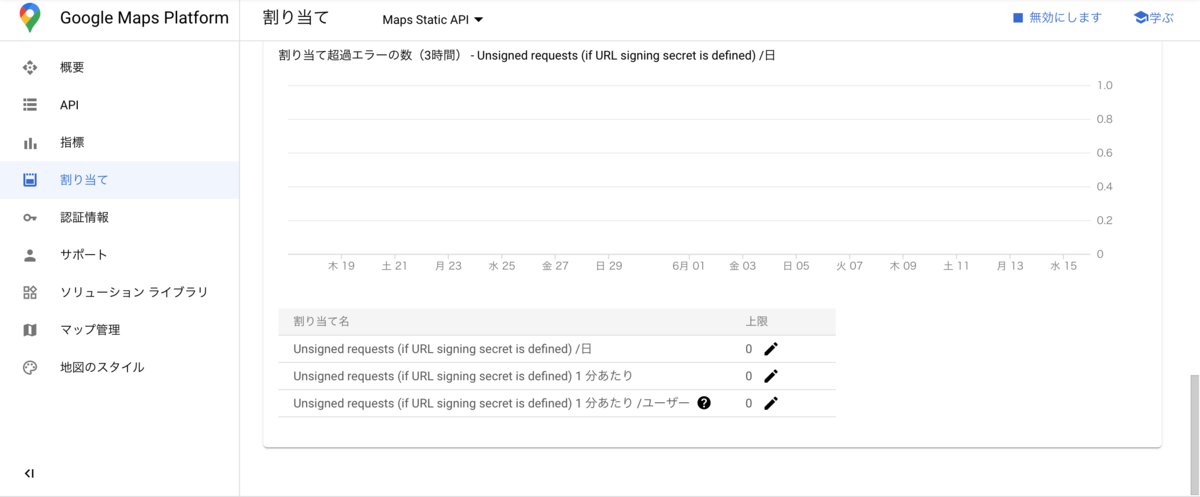
これで未署名のURLでリクエストを送ると

このような画像が返ってきました。制限できているっぽいです。

位置情報を付与した地図を取得する

やっとメインコンテンツです。

地図自体の表示はできているので、次はその地図に位置情報によるルート表示をしてみます。

これまでの地図表示のAPIにpathというパラメータを足すだけです。

pathのフォーマットは以下のようになっています。

path=weight:[WEIGHT]|color:[COLOR]|[LAT1],[LON1]|[LAT2],[LON2]|...

[WEIGHT]は表示するルートの線の太さです。 [COLOR]は線の色です。カラーコードや名称で指定できます。 [LAT1],[LON1]は位置情報です。|で繋げて複数の緯度経度を指定するとその位置を通る線を引っ張ります。

オプションは他にもあります。他のオプションについては公式Docを参照してください。

developers.google.com

他のオプションも|で繋いでいきます。

ただし、|はURLにおいて無効な文字なのでURLエンコードする必要があります。URLエンコードすると、| -> %7Cに変わります。

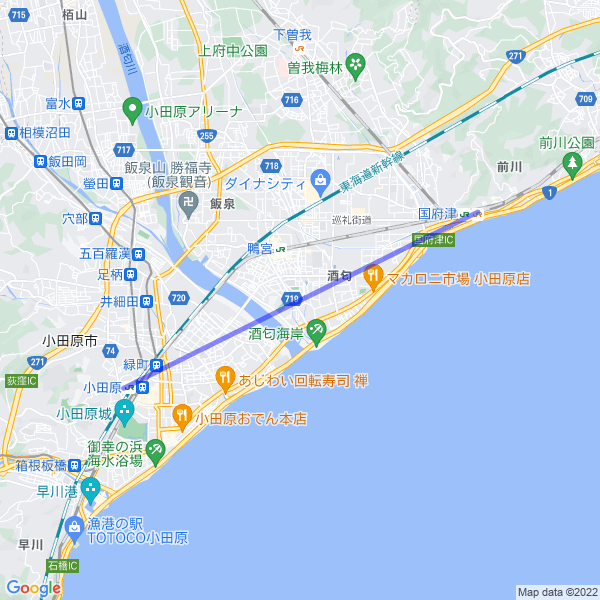
これを元に小田原駅(35.2564493,139.1532045)から国府津駅(35.2811428,139.2140066)までの線を引く地図は以下のURLで取得できます。

https://maps.googleapis.com/maps/api/staticmap?size=600x600&path=weight:5%7Ccolor:blue%7C35.2564493,139.1532045%7C35.2811428,139.2140066&key=[API_KEY]&signature=[SIGNATURE]

APIを叩くと以下のような画像を取得できます。

小田原駅から国府津駅まで線を引けているっぽいですね。

これを応用してStrava APIから取得した位置情報を地図に付加します。

冒頭で述べたとおり、Strava APIから返ってくる位置情報は緯度経度で表示されていません。

この文字列は緯度経度をPolyline Encoding と呼ばれるエンコーディングを行ったものです。

ちなみにGoogle Maps Static APIはこのPolyline Encoding による位置情報もそのままリクエストに渡せることができます。

developers.google.com

pathパラメータにencを足し、そこにPolyline Encoding による位置情報を与えます。 Polyline EncodingにはURLにとって無効な文字も含まれているため、URLエンコーディングする必要があります。

Polyline Encodingに含まれる文字はASCIIコードの64(@) ~ 126(~)でその中でURLにとって無効な文字は

www.ipentec.com

に載っています。

ちなみにPolyline EncodingにはURLにとって予約文字となる文字も含まれていますが、その文字はURLエンコーディングしないように注意してください。

これを踏まえて遠軽町から湧別町までのアクティビティを地図に表示するURLは

https://maps.googleapis.com/maps/api/staticmap?size=400x400&path=weight:5%7Ccolor:blue%7Cenc:wuakGe%60akZ%5B%60@SKe@FqBx@uB%60AoAt@YKf@A~@i@XDbAbGQPGh@sGdIyDfFuE%60GkBtBiF~GqDhEwBjAiS%7CEcC~@_Ax@aGdH%7DDhEeBfA%7DCp@aMj@mCSiDiA%7Bp@aXaA_AgEyGqAuAaz@cc@_C_B%7BF%7BFoBkAiCy@oDy@cCWgE@aCZsC~@yA%60AcBrBwCdF%7B@dAsAhA%7BAp@uAZuC@kBWeDy@aAa@qMsDe%7D@cX%7BDa@eCB_BPyCr@_A%5EgRtJqCbAaDb@%7DBAcHu@oCIOUI?OTcFX_E%7C@uBz@_NdHmCzB%7BCbEqMpTkDhEkE%7CDwVzRoEjE%7DAxBsC%7CFyBdG_ClIq@~AqBvC%7BArAgCrAs%5EbKgBz@cA%7C@sAnBcAnCk@fCSWMi@aCeAwGuDo%5EaReKwFwR%7BJ%7BMeHaAq@%7DAm@cC%7BAeDuA%5DDMj@DFDw@Wu@eDwAwFcDkMqGc@GsAFcA%60@gGvAyBl@yC~@%7D@b@c@t@aAhA%5Br@kDfEuAp@mH%7CBkAEg@m@mB%7BFS%5D_Ao@yAo@eBgAcIyDy@o@kDmB_@IOSwAk@sBsA%7BCqA%7DQ%7DJiBu@y@m@qDkB%7BCsAu@m@mHoDyCiBkKkFaE_C_Bs@wIoEcBiAcCcAsC?o@PsHd@cEf@iIf@yEf@oKVoFWqDa@oFiAoIgCaGsAwAUeCAgDl@sBdAgEnCqFfCyC%60A%7BEx@wENoD?eCOoFy@eHcCoE_CkDgCeEiEiCgDyVob@qCeF_C_EUQ_H%7DLmKqQaC%7DCyAoA_FiC%5BG%7BByAsAi@%7DEsCkHoDiH_EaKcFgAu@uOaIwEkCmLkGiOyHGM%7D@%5Dq@g@mAe@gGiDgO_I%7BBaAeHsD%7DBuAi@QaRaKq@Wu@i@%7B@WaCyAcAYyAcAaAYYYcA_@c@_@s@Wa@i@iA_@iC%7BA%7BAk@%7B@o@iEmBmCcBuB%7B@aDqB%5BAWTHC?YUYiA_@yBoAeAw@i@MWYgCoAoAg@m@i@aCiAc@_@w@QsC%7DAsA%7D@iBu@cGiDyAg@%5BYgD_B%5BY_@KwByAwCuAUWgFmC_DwAgAm@_Am@yAm@MSkDeBQUm@OmNoHmBkAy@WaAq@kAe@%7BDsBgAu@%7BBcAsDwBiD%7DAEMaAk@eCkAwA%7D@%5BGyBuAuKiFe@_@aIiEa@IkAk@k@g@u@WmB%7B@w@o@_By@kA_@g@e@i@Sg@a@w@WgB_A%5D%5By@%5DSYgA_@aBcA_AY%5CBFc@C_@Ji@Tu@NkAfAwET@zBpAb@@BFOT?L&key=[API_KEY]&signature=[SIGNATURE]

です。

これでリクエストすると

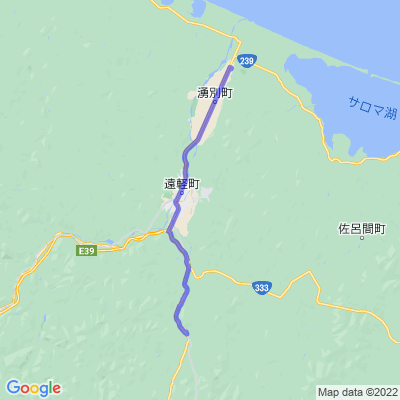
Stravaのスクショ通りの画像を取得できました。

おまけ

Polyline Encoding Algorithmについて

緯度経度からPolyline Encodingする具体的なフローについてです。

公式がPolyline Encodingの具体的な手順について載せています。

developers.google.com

小田原駅(35.2564493,139.1532045)から国府津駅(35.2811428,139.2140066)までの線をPolyline Encodingする例を考えます。

小田原駅から考えます。

まずは105して丸めます。

3525644,13915320

次に2の補数の2進数に変換します(32bit)。正の数なので変わりないです。

緯度: 00000000001101011100110000001100
経度: 00000000110101000101010010111000

1ビットの左へのシフト演算によって値を2倍する。

緯度: 00000000011010111001100000011000
経度: 00000001101010001010100101110000

この時点で負の数の場合はビットを反転させますが、今回は正の数なので操作はありません。

緯度: 00000000011010111001100000011000
経度: 00000001101010001010100101110000

変換した2進数を右から5ビットずつに分割します。溢れた分は消します。

緯度: 00000 00110 10111 00110 00000 11000
経度: 00000 11010 10001 01010 01011 10000

分割した5ビットの1単位をチャンクと呼びます。チャンクを逆順にします。

緯度: 11000 00000 00110 10111 00110 00000
経度: 10000 01011 01010 10001 11010 00000

左のチャンクから順番に0x20の論理和演算をします。 最後のチャンク(=次以降のチャンクが0)の場合はチャンク先頭に0を付加します。

緯度: 111000 100000 100110 110111 000110 000000
経度: 110000 101011 101010 110001 011010 000000

それぞれのチャンクを10進数に戻します。

緯度: 56 32 38 55 6
経度: 48 43 42 49 26

それぞれの値に63を足します。

緯度: 119 95 101 118 69
経度: 111 106 105 112 89

それぞれの値をASCIIコード*3として文字に変換します。

すると緯度経度それぞれ

緯度: w_evE
経度: ojipY

で表されます。

よって、小田原駅の緯度経度をPolyline Encodingすると w_evEojipYです。

実際にAPIを叩いてみると

https://maps.googleapis.com/maps/api/staticmap?&size=600x600&path=weight:5%7Ccolor:red%7Cenc:w_evEojipY&key=[API_KEY]&signature=[SIGNATURE]

小田原駅周辺の画像を取れました。

次に国府津駅のPolyline Encodingをしていきます。

入力する緯度経度が複数の場合2つ目以降は一つ前の緯度経度との差分を考えます。 つまり、 (35.2811428,139.2140066) - (35.2564493,139.1532045) = (0.00246935, 0.00608021) です。

105して丸めます。

2469,6080

次に2の補数の2進数に変換します(32bit)。

緯度: 00000000000000000000100110100101
経度: 00000000000000000001011111000000

1ビットの左へのシフト演算によって値を2倍します。

緯度: 00000000000000000001001101001010
経度: 00000000000000000010111110000000

正の数なのでビット反転はしません。

緯度: 00000000000000000001001101001010
経度: 00000000000000000010111110000000

変換した2進数を右から5ビットずつに分割する。溢れた分は消します。

緯度: 00000 00000 00000 00100 11010 01010
経度: 00000 00000 00000 01011 11100 00000

チャンクを逆順にします。

緯度: 01010 11010 00100 00000 00000 00000
経度: 00000 11100 01011 00000 00000 00000

左のチャンクから順番に0x20の論理和演算をします。 最後のチャンク(=次以降のチャンクが0)の場合はチャンク先頭に0を付加します。

緯度: 101010 111010 000100 00000 00000 00000
経度: 100000 111100 001011 00000 00000 00000

それぞれのチャンクを10進数に戻します。

緯度: 42 58 4 経度: 32 60 11

それぞれの値に63を足します。

緯度: 105 121 67
経度: 95 123 74

ASCIIコードに変換すると、 iyC_{J です。

URLに載せるときはURLエンコーディングして iyC_%7BJ になります。

小田原駅のPolyline Encodingと合わせると、

https://maps.googleapis.com/maps/api/staticmap?&size=600x600&path=weight:5%7Ccolor:red%7Cenc:w_evEojipYiyC_%7BJ&key=[API_KEY]&signature=[SIGNATURE]

APIを叩くと小田原駅から国府津駅の線が出ました。

*1:base64の違いは https://qiita.com/kunihiros/items/2722d690b1525813c45e を参考にしました

*2:HMAC-SHA1についてはhttps://e-words.jp/w/HMAC.htmlを参考にしました

*3:https://www.k-cube.co.jp/wakaba/server/ascii_code.htmlを参考にしました。

Strava APIを利用してツーリングのデータを取得できるようになるまで

Stravaとは

www.strava.com

Stravaは自転車やランニングなど走ったGPSログを共有することができるスポーツマン向けのSNSのようなものです(勝手な解釈)。

自分はツーリングやサイクリングなどのライドに行くときはサイクルコンピュータを起動してGPSでどこを走ったかなどを記録しています。

ライドが終わったあとは、このデータをアクティビティとしてStravaにアップロードしています。

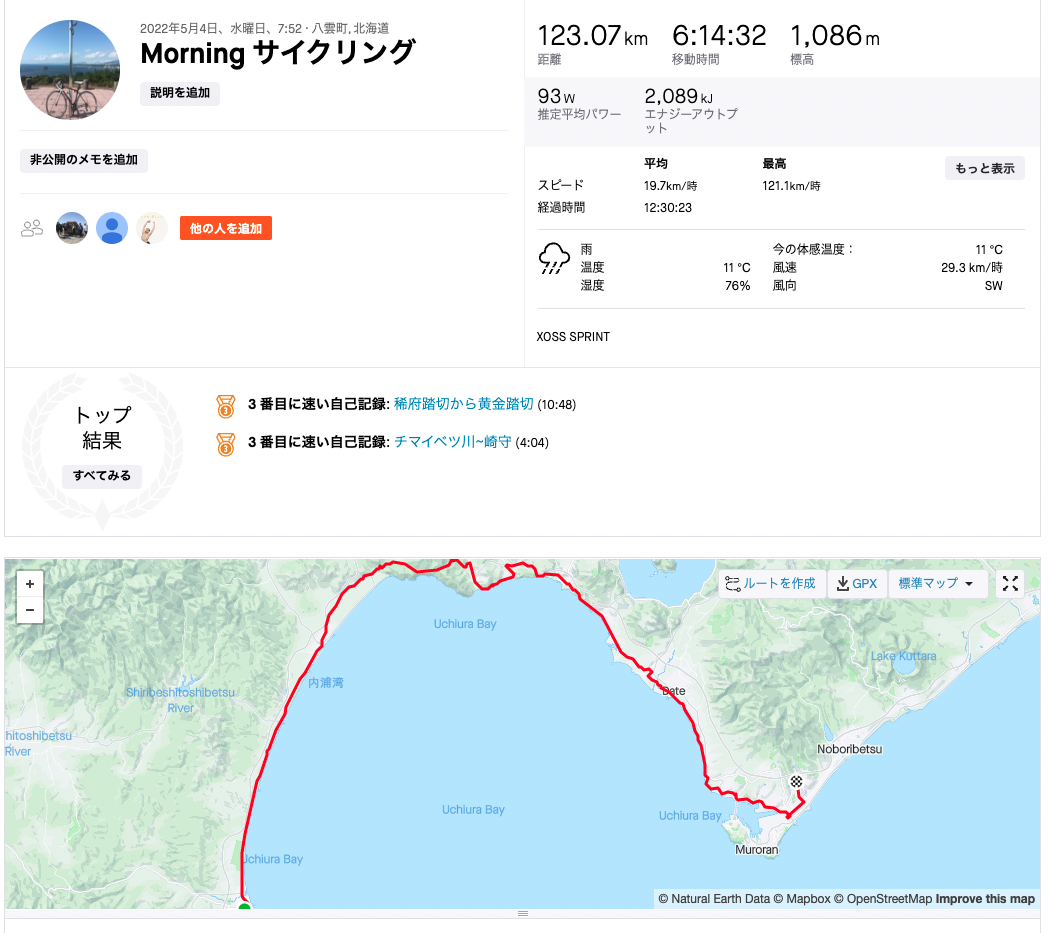
StravaのAPIはこれらのアクティビティをJSON形式で取得できます。

今回は今までのアクティビティを引っ張ってきて面白いことできないかなと思いAPIを使うことにしました。

ついでに自分のアカウントも載せておくか。

www.strava.com

APIを使えるようになるまで

最低限のスコープをもったアクセストークンの取得まで

この記事では、APIでアクティビティを取得できるまで説明するため

  • Stravaのアカウント
  • 最低1つのアクティビティ

が必要です。

持っていない人は新規登録してからひとっ走り行ってきてアクティビティをアップロードしてください。

伊豆大島がおすすめです

アカウントを持っている人は右上のアイコンから設定を押します。

設定画面を開いて左のメニューからMy API アプリケーションを選択します。

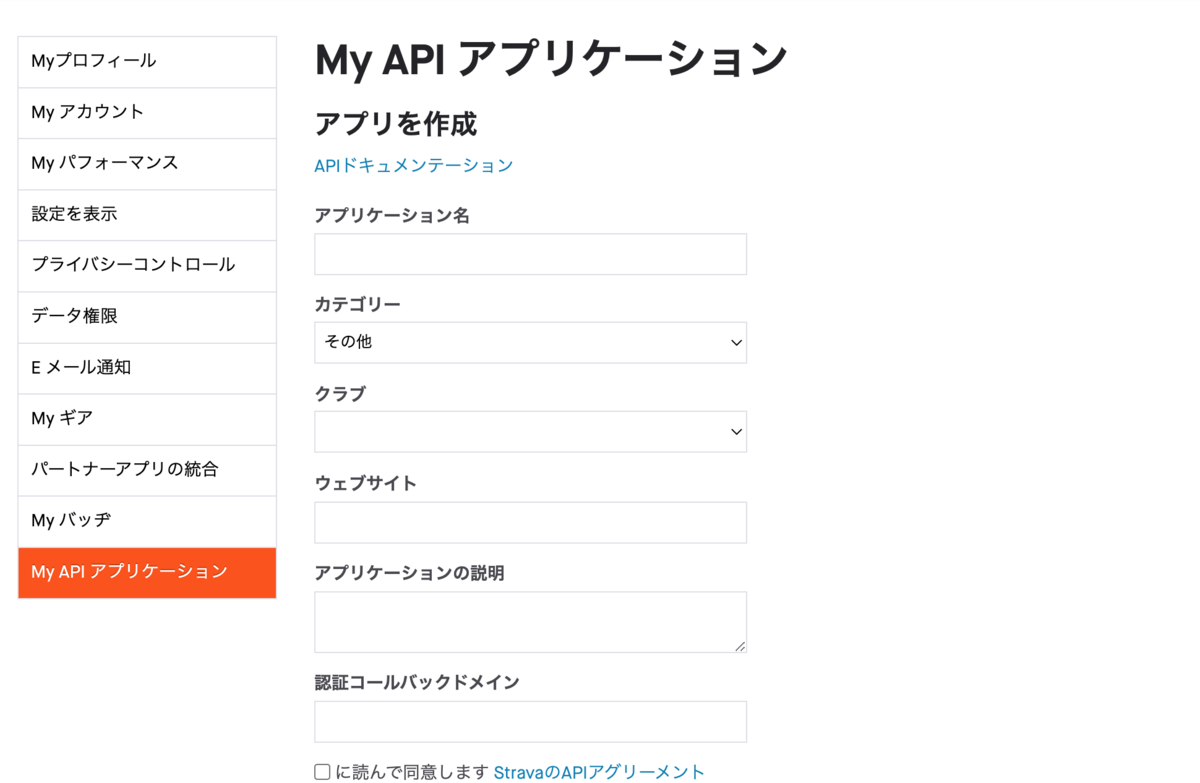
StravaのAPIを利用して開発する予定のアプリの情報を入力します。

まだ決まってない場合はこれらの情報をあとから変更できるのでとりあえず適当に入力します。

自分は適当に入力しました。

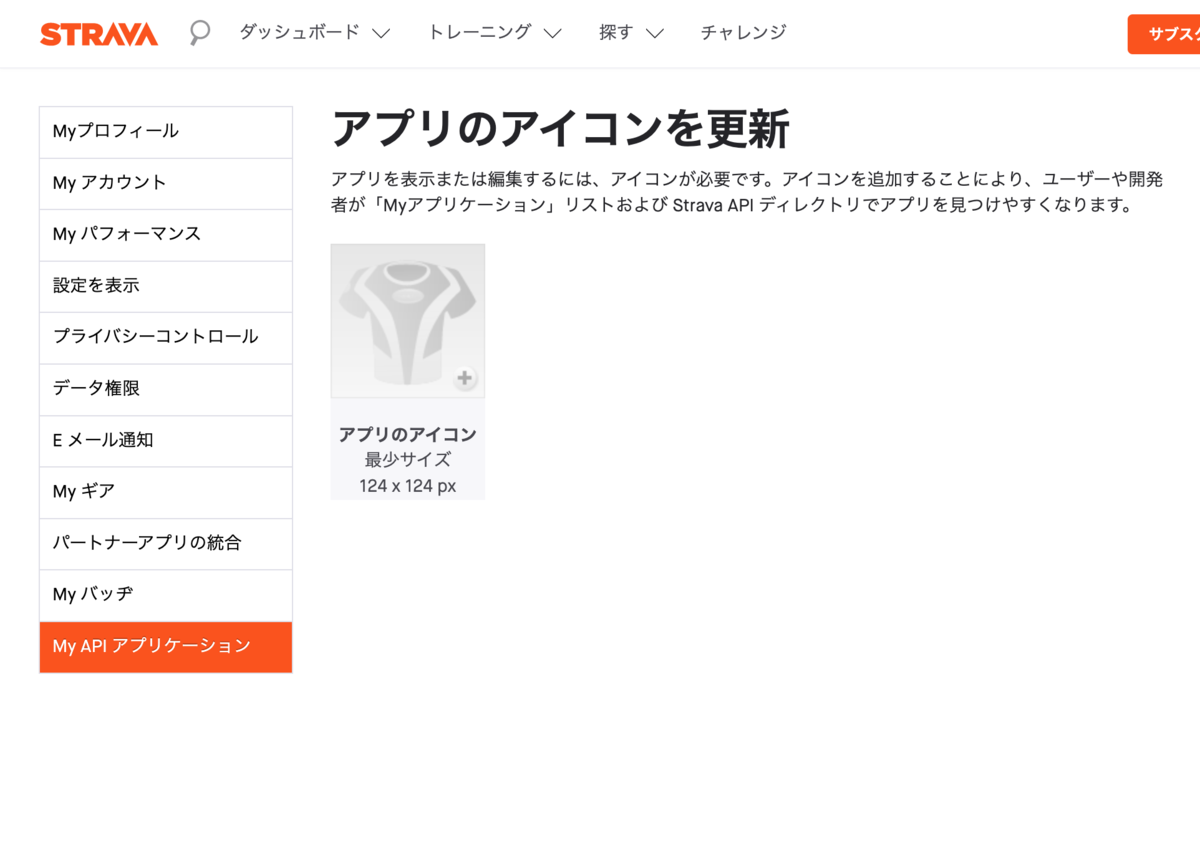
作成後、アプリのアイコンの設定が必要です。未設定のまま進められないので適当に設定します。

設定後、API利用に必要な各種パラメータが与えられます。

  • クライアントID
  • クライアントシークレット
  • アクセストークン
  • リフレッシュトークン

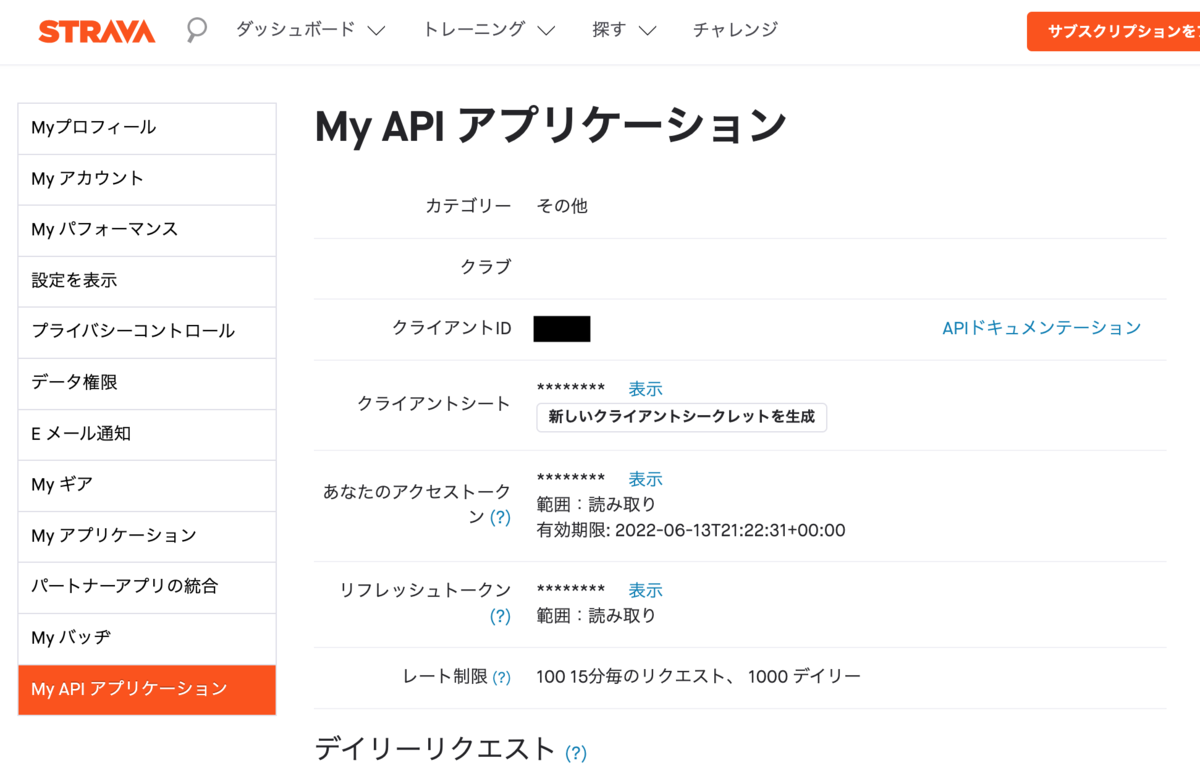
この中で、

  • クライアントID
  • クライアントシークレット

はずっと同じ値を使い続けますが

は有効期限があるので一定期間毎に変わっていきます。

今回の登録で取得したアクセストークンは認証に必要な最低限のスコープのみ与えられていて、叩けるAPIも限られています。

まずはアクセストークンが正しいか試します。

自分自身のプロフィール取得のAPIは現時点のスコープで叩けるので、取得したアクセストークンを使って取得してみます。

curl -X GET \ 
https://www.strava.com/api/v3/athlete \
-H 'Authorization: Bearer ${ACCESS_TOKEN}

${ACCESS_TOKEN}は自分のアクセストークンに書き換えてください。

実行するとレスポンスが返ってきます。

{"id":24719665,"username":"uhhyoi","resource_state":2,"firstname":"うっ","lastname":"ひょい","bio":"","city":"","state":"","country":"","sex":"M","premium":true,"summit":true,"created_at":"2017-09-03T09:46:56Z","updated_at":"2022-05-26T11:03:56Z","badge_type_id":1,"weight":62.0,"profile_medium":"https://dgalywyr863hv.cloudfront.net/pictures/athletes/24719665/7117793/2/medium.jpg","profile":"https://dgalywyr863hv.cloudfront.net/pictures/athletes/24719665/7117793/2/large.jpg","friend":null,"follower":null}%

Strava登録時に設定したプロフィールが返ってきます。

自分の体重などがバレてますが、まあ、現在はこれよりも痩せているので大丈夫です。

プロフィールが返ってきていたら成功です。

次にOAuth認証によって更に様々なAPIを叩けるアクセストークンとリフレッシュトークンを取得します。

OAuth認証

認証用のURLを組み立てる

以下のURLをベースにアクセスするURLを組み立てます。

http://www.strava.com/oauth/authorize?client_id=[REPLACE_WITH_YOUR_CLIENT_ID]&response_type=code&redirect_uri=http://localhost/exchange_token&approval_prompt=force&scope=activity:read

URL内の[REPLACE_WITH_YOUR_CLIENT_ID]は先程取得した自分のクライアントIDに置き換えます。 クエリパラメータにあるscope=activity:readには取得するアクセストークンのスコープを指定します。

指定できるscopeは developers.strava.com

公式のDocにあるDetails About Requesting Accessセクションのscopeの欄に記載があります。

現時点のscopeがreadしかないので、APIを通じて自分のアクティビティにはアクセスできません。

各APIを叩くために必要なscopeについてはAPIリファレンスに載っているので参照してください。

例えば、自分のアクティビティを一覧取得するAPIは

https://developers.strava.com/docs/reference/#api-Activities-getLoggedInAthleteActivities

Requires activity:read.

とあるので、アクセスするにはactivity:readというscopeが必要になります。

よってクエリパラメータにはscope=activity:readと指定します。

認証する

組み立てたURLにアクセスします。

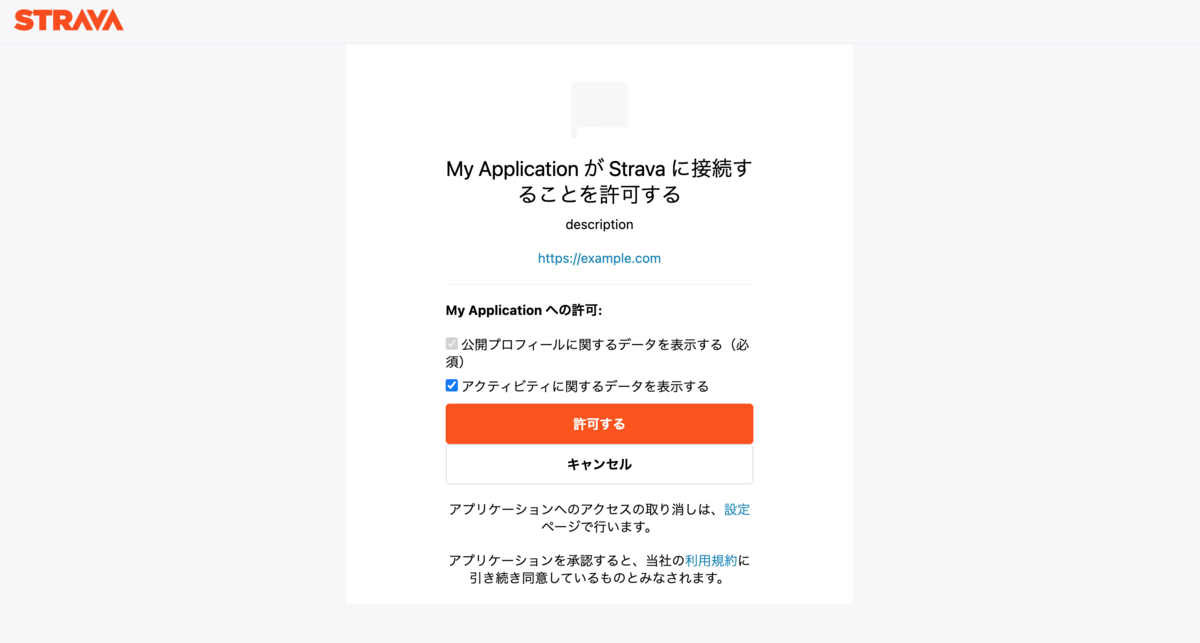
このような画面が出るので「アクティビティに関するデータを表示する」にチェックが入っていることを確認して「許可する」を押します。

するとリダイレクトされてそのURLにcodeというクエリパラメータが入っています。 このcodeを元に認証を進めます。

ちなみにリダイレクト先はlocalhostなので、「このサイトにアクセスできません」と表示されているのは正常です。

次に認証に必要なPOSTリクエストを以下のように投げます。

curl -X POST https://www.strava.com/oauth/token \
    -F client_id=${YOUR_CLIENT_ID} \
    -F client_secret=${YOUR_CLIENT_SECRET} \
    -F code=${AUTHORIZATION_CODE} \
    -F grant_type=authorization_code

${YOUR_CLIENT_ID},${YOUR_CLIENT_SECRET} にはそれぞれ最初に取得したクライアントIDとクライアントシークレットに置き換えます。

${AUTHORIZATION_CODE}はリダイレクト先に表示されていたクエリパラメータのcodeの値に置き換えます。

これでリクエストを送ると、以下のようなレスポンスが返ってきます。

{"token_type":"Bearer","expires_at":1655159199,"expires_in":21600,"refresh_token":"${REFRESH_TOKEN}","access_token":"${ACCESS_TOKEN},"athlete":{"id":24719665,"username":"uhhyoi","resource_state":2,"firstname":"うっ","lastname":"ひょい","bio":"","city":"","state":"","country":"","sex":"M","premium":true,"summit":true,"created_at":"2017-09-03T09:46:56Z","updated_at":"2022-05-26T11:03:56Z","badge_type_id":1,"weight":62.0,"profile_medium":"https://dgalywyr863hv.cloudfront.net/pictures/athletes/24719665/7117793/2/medium.jpg","profile":"https://dgalywyr863hv.cloudfront.net/pictures/athletes/24719665/7117793/2/large.jpg","friend":null,"follower":null}}%

${REFRESH_TOKEN},${ACCESS_TOKEN}は新しいスコープを持つリフレッシュトークンとアクセストークンです。

この新しいアクセストークンを使うことで自分のアクティビティを取得することができます。

早速、過去30件のアクティビティをAPIで取得してみます。

curl -X GET https://www.strava.com/api/v3/athlete/activities -H "Authorization: Bearer ${ACCESS_TOKEN}"

${ACCESS_TOKEN}は新しく取得しているアクセストークンです。

いろいろぐちゃぐちゃ返ってきたら成功です。JSON形式で返ってきているのでjqコマンドに通したりすると読みやすいと思います。

jqコマンド通したレスポンスの一部が以下です。

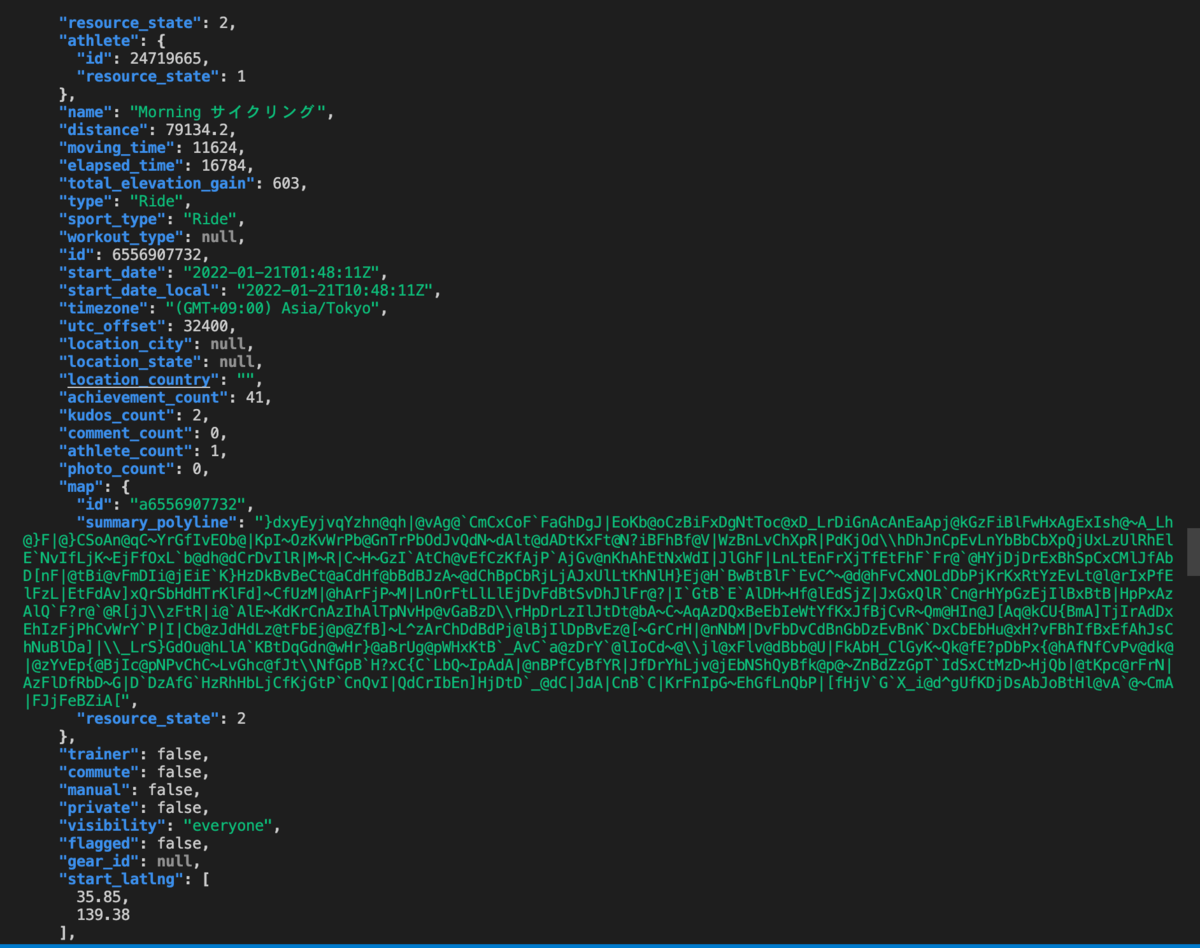
アクティビティっぽいデータが返ってきています。 ちなみにsummary_polylineというキーにあるグチャグチャ長い文字列はスタートからゴールまで走った位置情報をPolyline Encoding Algorithmという手法でエンコードしたものです。 デコードすると大量の緯度経度のデータになります。

各データの意味やAPIの利用方法は公式のリファレンスを参照してください。

developers.strava.com

これで一通りAPIが使えますが、注意点があります。

トークンのリフレッシュ

認証した際に返ってきたレスポンスに、expires_at, expires_inがありました。 これらはアクセストークンの有効期限を表しています。

{"token_type":"Bearer","expires_at":1655159199,"expires_in":21600,"refresh_token"...

expires_atは期限切れになる日時のUNIX Timeです。 expires_inはアクセストークンが持つ期間自体を秒で表したものです。 つまり 21600 / 3600 = 6  で6時間でアクセストークンは期限切れになります。

期限が切れたアクセストークンではAPIは叩けなくなります。

そのためアクセストークンのリフレッシュを定期的にする必要があります。

リフレッシュをすることでまた新たに同等のスコープのアクセストークンが発行されてそれをまた6時間使うことになります。

トークンのリフレッシュ方法は 公式DocのRefreshing Expired Access Tokensセクションに書いてあります。

developers.strava.com

以下のPOSTリクエストを送るだけです。

curl -X POST https://www.strava.com/api/v3/oauth/token \
  -d client_id=[YOUR_CLIENT_ID] \
  -d client_secret=[YOUR_CLIENT_SECRET]\
  -d grant_type=refresh_token \
  -d refresh_token=[YOUR_REFRESH_TOKEN]

[YOUR_CLIENT_ID],[YOUR_CLIENT_SECRET]は先程の認証で使ったものと同様のパラメータを使います。

[YOUR_REFRESH_TOKEN]はcodeを使って認証した際に取得したリフレッシュトークンに置き換えます。

StravaのMy APIアプリケーションに記載されているリフレッシュトークンは最低限のスコープに紐付いたリフレッシュトークンなので間違えないように気をつけてください。

置き換えてリクエストを投げると、認証のときと同様のレスポンスが返ってきます。

そのレスポンス内に新たなアクセストークンとリフレッシュトークンがあるのでAPIを投げるときはその新たなアクセストークンを使います。

そのアクセストークンも期限切れになったときは再びリフレッシュトークンを使って更に新しいアクセストークンとリフレッシュトークンを発行して使うといった流れになります。

プログラムを使ってAPIを叩くときは期限切れをチェックして自動的にトークンをリフレッシュするようにコードを書いておくのがおすすめです。

おわりに

これでStravaのAPIを使ってアクティビティを取得できます。このデータを取得してStrava側で集計して表示してくれないデータなどをプログラム組んで集計できたりします。

参考

Strava Developers

スポーツログアプリのStravaからAPIでアクティビティデータを取得してみる | DevelopersIO

日本列島をLaTeXで表示させたかったのでSVGをTikZに変換するプログラムを作った

この記事はTeX & LaTeX Advent Calendar 2019 16日目の記事です． 15日目は aminophenさんでした．17日目はt-kemmochiさんです．

はじめに

LaTeXは論文や理工系のレポートを書くのにとても特化したすばらしいツールです． また，様々なパッケージが提供されており，TeXとLaTeXだけで様々なものを作れます．

自分はこれまでそんなLaTeXを使っていろいろ遊んできました．

LaTeXで提供されているTikZという図を描画できるソフトでデレマスの名刺を作ったり muscle-keisuke.hatenablog.com

GPSのログをLaTeXで処理して表示した画像上にTikZでGPSの軌跡を表示したり muscle-keisuke.hatenablog.com

TeXで定義できるマクロを再帰的に呼び出せることを利用しTikZでフラクタル図形を描画したりしました． muscle-keisuke.hatenablog.com

さて，今回のテーマは

「日本列島をLaTeX(TikZ)のコマンドだけで描画してみる」です．

今年のAdvent CalendarのテーマはLuaLaTeXですが，全く守る気がありません．

きっかけ

CountriesOfEurope

CTANにはCountriesOfEuropeというヨーロッパ諸国を表示できるコマンドが定義されているパッケージがあります．

www.ctan.org

\documentclass{article}
\usepackage[Scale=7.5]{countriesofeurope}
\begin{document}
This is Germany $\rightarrow$ \EUCountry[Scale=3]{Germany}
\end{document}

もうこれだけでドイツが出ます．(もちろん他のヨーロッパ圏の国も出せます．) f:id:muscle_keisuke:20191211012542p:plain

しかし，ヨーロッパだけで自分が住んでいる日本がないのはとても悔しかったのです．

「なければ自分で作ればよい」

ということで，作ることにしました．

方針

自分の中で2つの方法が思い浮かびました． - 日本地図を目視で確認してTikZのコマンドを巧みに使って一から描いていく - ベクタ画像のテキストをTikZのコマンドに変換するスクリプトを作る

今回はスケジュールを見積もった結果2番目の方法が良さそうなので変換スクリプトを作ることにしました．

作っていく

まずは日本列島のベクタ画像を持ってくる

今回は画像をLaTeXの形式に変換するので，点で画像を構成しているラスタ画像ではなく，線で構成しているベクタ画像を持ってきます．

ここの画像を持ってきます． 画像形式はSVG形式です．SVGはScalable Vector Graphicsの略でXMLベースのスキーマで描画命令が書かれているベクタ画像の形式です．

https://d-maps.com/m/asia/japan/japon/japon04.svg

SVGだったのでSVGの描画命令を理解する

SVGを開くとテキストが以下のように羅列しています．

<path class="fil1 str0" d="M15159.54 1008.44l-433.65 0c8.17,33.38 12.53,58.06 17.98,92.12 4.78,30.66 17.04,45.65 24.53,76.3
 4.08,16.35 5.45,27.25 8.17,43.6 9.54,57.23 10.9,90.61 10.9,148.51 0,23.85 7.5,38.84 0,61.32 -2.72,8.86 -8.85,13.62 -13.62,21.79 
8.17,4.78 14.98,5.45 21.8,10.9 14.31,12.27 15.67,27.25 24.52,43.6 7.5,13.63 19.76,18.4 24.53,32.7 7.5,20.44 6.13,35.43 16.35,54.5 
7.5,14.31 19.76,18.4 29.97,29.98 17.04,18.4 29.3,27.25 51.78,38.15 3.41,-45.64 1.36,-73.58 21.8,-114.45 5.44,-11.58 5.44,-22.48 
13.62,-32.7 12.26,-14.99 32.7,-11.58 43.6,-27.25 6.81,-10.21 4.09,-21.11 8.17,-32.7 10.23,-27.25 22.49,-39.51 35.43,-65.4 
19.76,-40.19 25.89,-67.44 32.7,-111.72 2.05,-13.63 8.17,-21.8 8.17,-36.1l0 -85.84c0,-26.57 7.5,-41.56 16.35,-66.09 10.9,-29.97 
22.59,-52.61 36.9,-81.22zm
...
"/>

まずはこれらのテキストを読み解いてどういう描画を行っているのかを理解する必要があります．

以下のページを参考にSVGの描画命令について見てみました． triple-underscore.github.io

そうすると線の描画を行っているのは

<path class="fil1 str0" d="ここの部分"/>

d=の先の数字の羅列です．この数字の羅列をパスデータといいます． パスデータに含まれているアルファベットが直線を描くのか曲線を描くのかの命令になっています． アルファベットと描画命令の対応は以下のようになっています．

描画命令と引数 意味
M(x,y) 絶対座標(x,y)に描画点を移動する
L(x,y) 現在の描画点から絶対座標(x,y)に直線を描画する
C(x1,y1,x2,y2,x,y)+ 現在の描画点から絶対座標(x1,y1),(x2,y2)を制御点として(x,y)まで三次ベジェ曲線を描画する，3つ以上引数に取ることができて，その後の引数は第一制御点，第二制御点，曲線の終点の座標の順番を繰り返し指定する．
z(引数なし) 線を閉じるように直線を引く

それぞれの大文字に対応する小文字は引数に取る座標が現在の描画点に対する相対座標となります． また，引数の間はカンマでも空白でも認識されます． つまり

<path class="fil1 str0" d="M15159.54 1008.44l-433.65 0c8.17,33.38 12.53,58.06 17.98,92.12 4.78,30.66 17.04,45.65 24.53,76.3

というパスデータをアルファベット毎に改行すると

M15159.54 1008.44
l-433.65 0
c8.17,33.38 12.53,58.06 17.98,92.12 4.78,30.66 17.04,45.65 24.53,76.3

となり，絶対座標(15159.54, 1008.44)を開始点とし，そこから相対座標(-433.65, 0)へ直線を引き第一制御点を相対座標(8.17,33.38) ，第二制御点(12.53,58.06)，曲線の終点(17.98,92.12)の三次ベジェ曲線，第一制御点を相対座標(4.78,30.66) ，第二制御点(17.04,45.65)，曲線の終点(24.53,76.3)の三次ベジェ曲線を引く という命令になります．

3次ベジェ曲線とは

開始点P 第一制御点Q 第二制御点R 終点S としたとき PQ,QR,RSをt:1-tで内分したときのそれぞれの内分点P',Q',R'を結んだ P'Q',Q'R'を更にt:1-tで内分した点P'',Q''を結んだ点をt:1-tで内分した点の集合で描画される曲線(tを0から1動かしたときの軌跡)

以下のサイトは手書きでベジェ曲線を描いていてわかりやすいと思います．

nixeneko.hatenablog.com

SVGの命令を文字列処理してTikZに変換するプログラムを作る

SVGの命令がわかったところで，これをTikZに変換するプログラムを作っていきます．

Perlで作る(LaTeXでやれや)

現在，業務でPerlを使うことが多いので練習がてらPerlを使って作ることにします． いつもならLaTeXで全部実装するところなんですが，時間がないのでPerlでちゃちゃっと作っちゃいます．

SVGの命令とTikZのコマンド対応を考える

SVGの命令は先程の表の通りです．対応するTikZのコマンドは

描画命令と引数 意味 TikZコマンド
M(x,y) 絶対座標(x,y)に描画点を移動する | start_x,start_y,current_x,current_yにx,yを代入する
L(x,y) 現在の描画点から絶対座標(x,y)に直線を描画する \draw(current_x, current_y) -- (x, y);
C(x1,y1,x2,y2,x,y)+ 現在の描画点から絶対座標(x1,y1),(x2,y2)を制御点として(x,y)まで三次ベジェ曲線を描画する，3つ以上引数に取ることができて，その後の引数は第一制御点，第二制御点，曲線の終点の座標の順番を繰り返し指定する． \draw (current_x, current_y) .. contorols (x1, y1) and (x2, y2) .. (x, y);
z(引数なし) 線を閉じるように直線を引く \draw (current_x, current_y) -- (start_x, start_y);

current_x, current_yは現在の描画点の座標start_x,start_yは描画開始した際の一番最初の座標です．

SVGは現在の描画点を内部的に保存して次の線を引きますが，TikZは線を引くたびに引き始めの座標を指定する必要があるのでプログラムの変数で保存しておく必要があります．

なので，描画点を決めるM(x,y)の命令が来たときにstart_x,start_y,current_x,current_yを代入するようにします．

原寸大はでかすぎてタイプセットできない

<path class="fil1 str0" d="M15159.54 1008.4...

のように最初から1万超えの座標から描画するとLaTeXはすぐに描画できなくなります． なので，TikZに変換するときに縮小して計算して，TikZのコードを生成します．

Perlで実装していく

SVGファイルを読み込む

sub load_SVG_file {
    my $file_name = shift;

    die 'Can\'t open file !' unless(
        open(
            my $svg, '<', $file_name
        )
    );
    my $svg_code = do {local $/; <$svg>};
    close $svg;

    return [ split(/\n/, $svg_code) ];
}

ファイルから読み込んだテキストから描画命令を分割する

sub read_path_list {
    my $svg_lines = shift;

    return grep { 
        $_ =~ /<path class=/ 
    } @$svg_lines;
}

<path class=...に描画に関する情報があるので，パターンマッチで取り出します．

sub get_svg_opes {
    my $svg_info = shift;

    $svg_info =~ /<path class=.*d="(.*)"\/>/;
    my $coodinates_string = $1;

    return [ split(/(?=[a-zA-Z])/, $coodinates_string) ]; # 肯定的先読み
}

正規表現を使って描画命令(アルファベット)毎に文字列を分割しますが，分割文字を消したくはないので肯定的先読みで分割した上でアルファベットを残します．

abicky.net

取得した描画命令によって分岐する

sub convert_tikz_from_svg_opes {
    my ($svg_opes, $scale) = @_;

    my $start_point = [0, 0];
    my $current_point = [0, 0];
    my $output_code = '';

    for my $cursor (@$svg_opes) {
        if ($cursor =~ /M/) {
            $current_point = fetch_abs_point($cursor, $scale);
            $start_point = $current_point;
        }
        elsif ($cursor =~ /m/) {
            $current_point = fetch_rel_point($cursor, $current_point, $scale);
            $start_point = $current_point;
        }
        elsif ($cursor =~ /l/) {
            my $converted = fetch_draw_line_ope($cursor, $current_point, $scale);
            $current_point = $converted->{new_point};
            $output_code .= $converted->{tikz_ope};
        }
        elsif ($cursor =~ /c/) {
            my $converted = fetch_draw_cubic_bezier_curve_ope($cursor, $current_point, $scale);
            $current_point = $converted->{new_point};
            $output_code .= $converted->{tikz_ope};
        }
        elsif($cursor =~ /z/) {
            my $converted = fetch_close_path_ope($current_point, $start_point);
            $current_point = $converted->{new_point};
            $output_code .= $converted->{tikz_ope};
        }
    }
    return $output_code;
}

M(描画点を指定の絶対座標に移動する)

sub fetch_abs_point {
    my ($ope, $scale) = @_;
    $ope =~ /M(-?[0-9.]*)[ ,](-?[0-9.]*)/;

    return [$1*$scale, $2*$scale];
}

m(描画点を指定の相対座標に移動する)

sub fetch_rel_point {
    my ($ope, $current_point, $scale) = @_;
    $ope =~ /m(-?[0-9.]*)[ ,](-?[0-9.]*)/;

    return [($1*$scale + $current_point->[0]), ($2*$scale + $current_point->[1])];
}

l(現在の描画点から指定の相対座標に直線を引く)

sub fetch_draw_line_ope {
    my ($ope, $current_point, $scale) = @_;
    $ope =~ /l(-?[0-9.]*)[ ,](-?[0-9.]*)/;
    my $tikz_ope = sprintf(
        "\\draw (%f, %f) -- (%f, %f);\n",
        $current_point->[0],
        $current_point->[1],
        $1*$scale + $current_point->[0], $2*$scale + $current_point->[1]
    );
    return +{
        new_point => [($1*$scale + $current_point->[0]), ($2*$scale + $current_point->[1])],
        tikz_ope  => $tikz_ope
    };
}

c(現在の描画点から指定した第一制御点，第二制御点を元に指定した相対座標まで三次ベジェ曲線を引く)

sub fetch_draw_cubic_bezier_curve_ope {
    my ($ope, $current_point, $scale) = @_;
    my $tikz_ope = '';
    while(
        $ope =~ /(-?[0-9.]*),(-?[0-9.]*) (-?[0-9.]*),(-?[0-9.]*) (-?[0-9.]*),(-?[0-9.]*)/g
    ) {
        $tikz_ope .= sprintf(
            "\\draw (%f, %f) .. controls (%f, %f) and (%f, %f) .. (%f, %f);\n",
            $current_point->[0], $current_point->[1],
            $1*$scale + $current_point->[0],
            $2*$scale + $current_point->[1],
            $3*$scale + $current_point->[0],
            $4*$scale + $current_point->[1],
            $5*$scale + $current_point->[0],
            $6*$scale + $current_point->[1]
        );
        $current_point = [($5*$scale + $current_point->[0]), ($6*$scale + $current_point->[1])];
    }
    return +{
        new_point => $current_point,
        tikz_ope  => $tikz_ope
    };
}

z(現在の描画点から引き始めの描画点まで閉じるように直線を引く)

sub fetch_close_path_ope {
    my ($current_point, $start_point) = @_;
    my $tikz_ope = sprintf(
        "\\draw (%f, %f) -- (%f, %f);\n",
        $current_point->[0],
        $current_point->[1],
        $start_point->[0],
        $start_point->[1]
    );
    return +{
        new_point => $start_point,
        tikz_ope  => $tikz_ope
    };
}

最後にTeXファイルに出力する

sub save_TeX_file {
    my ($file_name, $save_texts) = @_;
    die 'Can\'t open file !' unless(
        open(
            my $tex, '>', $file_name
        )
    );
    print $tex $save_texts;
    die 'Can\'t close file' unless(
        close $tex
    )
}

出力結果はこんな感じです．

\draw (151.595400, 10.084400) -- (147.258900, 10.084400);
\draw (147.258900, 10.084400) .. controls (147.340600, 10.418200) and (147.384200, 10.665000) .. (147.438700, 11.005600);
\draw (147.438700, 11.005600) .. controls (147.486500, 11.312200) and (147.609100, 11.462100) .. (147.684000, 11.768600);
\draw (147.684000, 11.768600) .. controls (147.724800, 11.932100) and (147.738500, 12.041100) .. (147.765700, 12.204600);
\draw (147.765700, 12.204600) .. controls (147.861100, 12.776900) and (147.874700, 13.110700) .. (147.874700, 13.689700);
\draw (147.874700, 13.689700) .. controls (147.874700, 13.928200) and (147.949700, 14.078100) .. (147.874700, 14.302900);
\draw (147.874700, 14.302900) .. controls (147.847500, 14.391500) and (147.786200, 14.439100) .. (147.738500, 14.520800);
\draw (147.738500, 14.520800) .. controls (147.820200, 14.568600) and (147.888300, 14.575300) .. (147.956500, 14.629800);
...

 よさそう． 早速，\inputで読み込んで出力してみます．

\documentclass[dvipdfmx]{standalone}
\usepackage{tikz}
\begin{document}
  \begin{tikzpicture}
    \input{island}
  \end{tikzpicture}
\end{document}

逆さまの日本列島

これで生成してみると逆さまの日本列島が出ました． これは座標系がSVGとLaTeXで違うのが原因だと考えられます． f:id:muscle_keisuke:20191214210114p:plain

y軸の正負を逆にする

Perlで変換する際のy軸の正負を逆にして出力します． f:id:muscle_keisuke:20191215220309p:plain

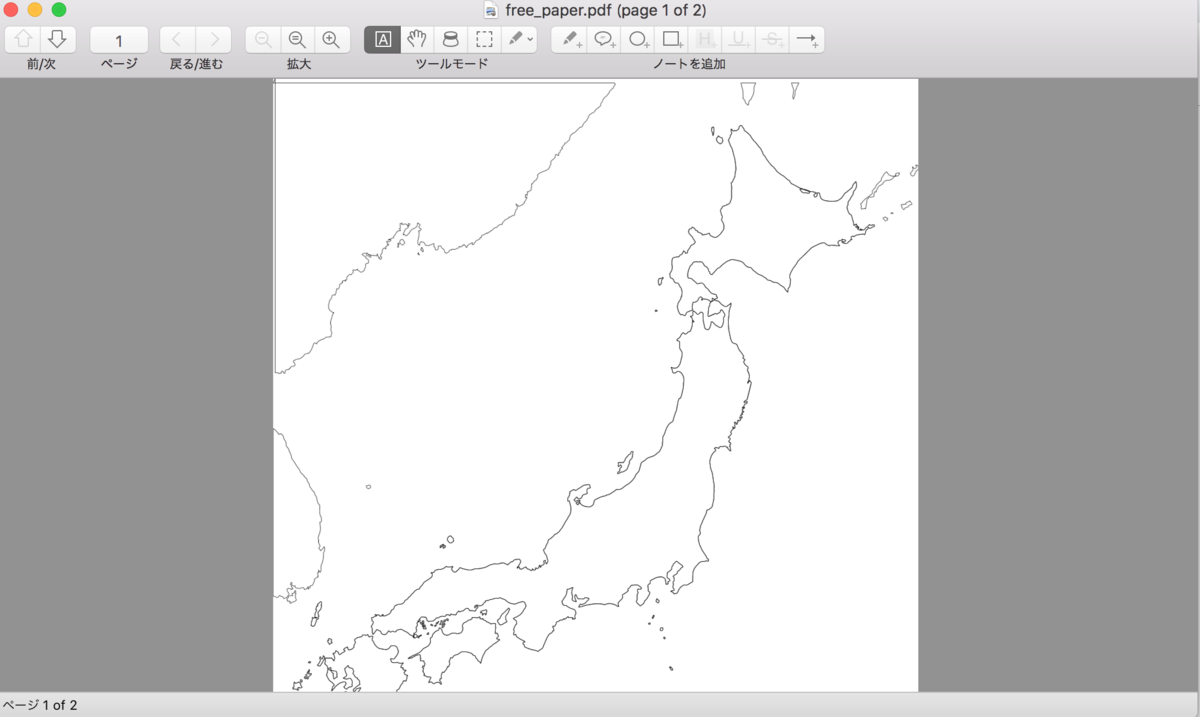
できた．

まとめ

ベクタ画像であるSVGも全てファイルはバイナリではなくテキストなので，簡単に変換できました．

汚いソースコードですが，一応，作ったものなので公開します．

Perl script for convert to SVG to TikZ

1年前のツーリングを振り返る 北海道1周ツーリング 13日目

蚊に刺されすぎて気が狂いそうになる

朝起きると，体中ぼこぼこに蚊に刺されまくっていました．

多分これまでの人生で最多刺されたと思います．

体をかきむしりながら札幌を出発しました．

初先頭

札幌から小樽まで走り，小樽は少しも観光せず，余市町まで行きました．

今では集団走行初心者ということで先頭が免除されてましたが，今ではグループが3人になってしまい， 2人の負担が大きくなってしまうので，自分も先頭を引くことになりました．

ハンドサインなどがちゃんと出せるか不安でしたが，特にトラブルもなく引くことができました．

自分は余市町のセブンイレブンから積丹町のウニ丼のお店まで引きました．

ウニ丼のお店

積丹町といえば，ウニが有名です． その中でも「お食事処 みさき」というお店は割と人気なので自分たちもそこに行くことにしました．

昼過ぎに到着したので，ウニ丼はすでに売り切れでした． 自分はウニがそれほど好きではないのでダメージはなかったですが，他のメンバーはがっかりしていました．

自分はいくら丼を頼みました． いくらがキラキラ光っていてとてもキレイでした．

もちろん美味しかったです．

見事な積丹ブルー

満足したところで先に進みました．この先は少し道をそれると神威岬という岬があります．

何もないというか車が通らない

セイコーマートがない町村

漁港

#

走った距離

トンネルでGPSが狂ったので実際は124kmくらい

1年前のツーリングを振り返る 北海道1周ツーリング 12日目

雷

テントで寝てる間も雨が土砂降りだったようでした．

明け方には雷が何度も鳴っていて，そのうちの一つはテントの近くに落ちて振動が来たくらいでした．

初パンク

今日は滝川にある大盛りメニューで有名な「マリン」というお店に行く予定です．

10時開店だったのでしばらくテントの中でゴロゴロしていると晴れてきました．

10時になるちょっと前に出発しようとした時，自分の自転車の異変に気づきました．

なんと，前輪の空気がまったくありませんでした．

ツーリング始まって以来の初めてのパンクでした．

急いでチューブを交換しましたが，交換して空気を入れた頃にはとっくに10時は過ぎてました．

マリン

泊まっていた公園から1.5kmくらいのところにあるのですぐ着きました．

とても派手な外見をしているのですぐわかりました． f:id:muscle_keisuke:20190822012301j:plain

席に通されてメニューを見てみると至って普通の品揃えと値段でした．

自分はカツカレーの普通盛り(850円)にしました．

できるまでは時間がかかるので，先程，修理したタイヤの空気を入れに外に出てました．

しばらくすると，カレーができたらしいので戻ってみると，

そこには

茶色い海がありました． f:id:muscle_keisuke:20190822012329j:plain

食いきれるか不安でしたが，毎日走ってお腹空いていていたので30分もかからずに平らげてしまいました． f:id:muscle_keisuke:20190822234214j:plain

まだ，お腹に余裕があったので，パフェもみんなで分け合って食べました． f:id:muscle_keisuke:20190822234339j:plain

美味しいし，安いし，大きいのでまた来たいと思えるお店でした．

お別れ

ここで，また一人メンバーとお別れになります．

稚内で膝を壊してしまったメンバーがこの後の日本縦断に備えて室蘭に直帰することになりました．

お互いにマリンの前でお別れをしました．

これで自分達の方は3人になってしまいました．

この期間がツーリングの中で一番人数が少なかった期間になります．

35km間コンビニなし

ひたすら国道275号線を走って札幌に向かいます．

辛いのはこの国道275号線には滝川市から月形町までの35km区間にコンビニが全くないことです．

起伏もないただ田んぼしかない道を35kmはかなりお尻も痛くて大変でした．

ちなみに2019年の6月くらいに滝川市と月形町の間にある浦臼町にローソンができたらしいです．

しかも，このローソン24時間営業じゃないんですね．

なぜか，この辺にはセイコーマートができずにローソンばっかりできるイメージがあります．

ついに札幌へ

月形町，当別町を抜けていくと，国道275号線とバイパスである国道337号線にぶち当たります．

ここでバイパスに乗り換えて札幌市内に向かっていきます．

しばらく走っていると，石狩川に架かる札幌大橋に差し掛かります．

ここから見える学園都市線の鉄橋が石狩川に反射してとてもキレイでした． f:id:muscle_keisuke:20190822012356j:plain

この札幌大橋を越えると札幌市に入ります．

北海道科学大学

今日は小樽市まで行く予定でしたが，札幌市で泊まることにしました．

札幌市内のセイコーマートで休んでいると近くに北海道科学大学があることがわかりました．

今日はもう走らないので見学がてら行ってみることにしました．

最近建て替えたばっかりらしくとてもきれいな建物でした． f:id:muscle_keisuke:20190822012423j:plain

手稲区に感動する

明日の朝ご飯を買いに手稲区にある複合商業施設に行きました．

それまでセイコーマートしかない街ばかり見ていたので 「すげー！一つの建物で100円ショップもあるしトライアルもあるのかよ！しかも同じ敷地に松屋まであるじゃん！」というこの十数日に田舎者からド田舎者になっていました．

とりあえず，この12日間で爪がかなり伸びてきていたので爪切りと明日の朝ご飯を買いました．

今日も自炊はせず松屋を食べて近くのスーパー銭湯に行きました．

地獄の公園

手稲区にある大きな公園に泊まることにしたのですが，この公園は今後の日程も含めて自分の中でワーストワンの公園でした．

トイレがめちゃくちゃ汚くて，蚊がめちゃくちゃ多かったです．少し歩くだけで蚊の壁にぶつかる感じです...

蚊取り線香も焚いたのですが，効果は今ひとつでした．

走った距離